This is the first of several blog posts meant to serve as a crash course in Haskell for someone already familiar with programming and somewhat familiar with functional programming. The next post can be found here.
Getting Started with Haskell
Time to get started! In this section, we’ll go over what Haskell is, what the audience of this guide is, and work up to our first complete Haskell program.
Haskell and You
You’re here to learn (or learn about) Haskell. Before getting into the nitty-gritty details of syntax and semantics, let’s briefly go over who you are and what Haskell is.
Haskell is a general-purpose statically-typed pure functional programming language. Let’s break that down:
-
General Purpose: A general purpose programming language is one not designed for any specific task in mind. For instance, SQL and LaTeX are domain-specific languages for database queries and document typesetting, respectively, while languages such as Java, Python, C++, and Haskell are designed for any sort of programming.
-
Statically-Typed: The meaning of a Haskell program is split into two phases — compile time and run time (similar to Java and C++). At compile-time, each variable has a type which indicates what sort of data that variable is allowed to hold. When you compile your program, Haskell enforces that all uses of variables respect the types those variables must have; if the program doesn’t respect the variable types, the Haskell compiler will produce error messages. Examples of statically typed languages include Java and C, while languages such as Python, Ruby, and PHP are dynamically typed (all variable types are checked at runtime).
-
Pure: Functions in a pure programming language (such as Haskell) will always produce the same output if given the same input. In other words, using a function multiple times on the same arguments is guaranteed to produce the same value. By default, functions may not perform side effects (such as file I/O or mutation of mutable values).
-
Functional: A functional language allows treating functions as values. You can create anonymous functions, store them in variables, pass them as arguments to other functions, and so on. Functional languages usually do not distinguish between statements and expressions, having only the latter. Statements are replaced by expressions that have some side effects when evaluated; however, they still return some value, like all expressions.
Haskell is a fairly unusual language. Many people liken learning Haskell to learning to program all over again; do not be discouraged if it takes a long time and a lot of effort. For many programmers, picking up a new language is a matter of finding an interesting project and implementing it in their new language of choice; while this is possible with Haskell, many aspects of the language require a more dedicated sort of study.
Now that we’re acquainted with Haskell, who are you? For the purposes of this guide, you are a somewhat experienced programmer who has worked with static type systems and functional languages and has a few years of general programming experience under their belt. Knowing languages such as Scheme, ML, OCaml may be helpful. If you don’t quite fit this bill, you may find parts of this guide to be very difficult. In this case, books on Haskell such as Learn You a Haskell and Real World Haskell may be useful to supplementing your understanding.
Haskell Programming Tools
The Haskell language has gone through several revisions. It was initially designed to be a standard for researchers exploring new programming language features. The first few iterations were the realm solely of researchers; modern Haskell really began with the Haskell 98 language standard. Several extensions were integrated into the standard later, leading to the Haskell 2010 language standard.
Although there are several Haskell compilers, GHC (the Glasgow Haskell Compiler) is by far the most commonly used and most featureful. Many extensions to the Haskell language are implemented only in GHC, so for the rest of this guide, you can assume that "Haskell" really means "Haskell with all the extensions and libraries that GHC offers".
With that in mind, let’s get started! Install GHC, open a text file in your favorite editor, and
enter the following program in a file called Test.hs (or another with the same extension):
module Test(main) where (1)
main = (2)
putStrLn "Hello" (3)| 1 | Declare a module named Test, and export the main function from it. Modules should be named
the same as their filenames. |
| 2 | The main function is the entry point to the program. The main module can be anything with a
main function. |
| 3 | The function putStrLn prints a string to standard output. Strings must be written with double
quotes; single quotes are used for single characters. |
Next, compile this with GHC by entering the following command into your shell:
ghc Test.hs -o my-program (1)| 1 | The -o flag tells ghc to write the final executable to a file called my-program. |
Note that the precise command may differ depending on your operating system and environment. The commands presented here should work under most Unix-like operating systems (Linux and Mac OS X), and serve as a good template for commands for other systems.
If you run this, you should see your program printing "Hello", as expected:
$ ./my-program
HelloCongratulations! You’ve written your first Haskell program. This program is deceptively simple, and in the next few sections we’ll explore what exactly this program does and how it does it, as well as look at many other features of the Haskell language.
Values and Functions
Next, we’ll dive quickly into Haskell language features. We’ll look at types and how you interact with the type system, creating global and local variable declarations, pattern matching on literals, and defining and creating functions. Try out code snippets as you read, and try your best to work through any error messages the compiler gives you. There’s a lot of ground to cover, so if it doesn’t all sink in immediately, don’t worry — there are exercises at the end of the section meant to ensure that you can use this material.
The Type System
Let’s take a look at another small Haskell program:
integer = 3
str = "Hello, World!"
character = 'C'
tuple = (integer, str, character)
main = print tuple (1)| 1 | The print function can be used to print many Haskell data types to the standard output. You
could also write print integer or print string; we will discuss these sorts of polymorphic
functions later. (A polymorphic function is one which operates on different types of data.) |
In this program, we declare four values: an integer, a string, a character, and a tuple containing three of these. Each of these has a different type. Note that all values in Haskell have some sort of type; there cannot be a value without a type. We don’t always have to write what the types are, though, because the compiler can look at how a value is used and guess what type it must have. Although the compiler is smart enough to infer the types for this simple program, we can explicitly annotate each top-level declaration with a type signature as well.
integer :: Int (1)
integer = 3
str :: String
str = "Hello, World!"
character :: Char
character = 'C'
tuple :: (Int, String, Char) (2)
tuple = (integer, str, character)
main :: IO () (3)
main = print tuple| 1 | Type annotations are written using the double-colon operator. integer :: Int is a type
declaration which tells GHC that the top-level variable named integer must be of type Int. |
| 2 | The type of a tuple consists of the types of its components. Since our tuple has an integer, a
string, and a character, the type of the tuple is (Int, String, Char). |
| 3 | The type of main is somewhat strange, and we’ll discuss this in detail eventually. All
functions which have a side effect (reading or writing files, printing to the console, and so on)
will have the IO type in their signature. |
More likely than not, when you start programming Haskell, you will find that the type system gets in your way. However, as you get used to Haskell and its type system, you will find that the type system and the compiler is a huge resource. You will be able rely on the type system to catch many common programming errors - in some ways, it will be like you have a friend watching over your shoulder as you write code, pointing out mistakes that are obvious in retrospect.
| By convention, all top-level values should have a corresponding type declaration, like in our second program. This improves the quality of error messages and forces you to double-check your types as you write code. Advanced programmers will actually start by writing all the top-level type declarations and filling out the values second. |
In order to use the type system, you can annotate values with types and write type declarations. In the example program above, we wrote a type declaration for every top-level value declaration we had. However, we could also have annotated every value:
integer = 3 :: Int (1)
str = "Hello, World!" :: String
character = 'C' :: Char
tuple = (integer, str, character) :: (Int, String, Char)
main = print tuple :: IO ()| 1 | Type annotations are of the form value :: type, with the double-colon coming directly after
the value itself. If you want to annotate only part of an expression, make sure you put parentheses
around the whole thing. For instance, 1 + 2 :: Int is equivalent to (1 + 2) :: Int, so if you
wanted to only annotate the 2, you would write 1 + (2 :: Int). |
Local Variable Bindings
We’ve already seen top-level value declarations along the following lines:
integer = 3However, there’s no reason that these values must be expressed using just literals, even if they
aren’t functions. For example, we can use a where clause to use some local variable bindings:
integer = one + two
where (1)
one = 1 (2)
two = 2| 1 | The where comes after the declaration it’s attached to, and is indented by two spaces. |
| 2 | The bindings declared in the where block must be aligned; one and two both start
at the same level of indentation. Both must be indented past the where itself as well. |
Computing the values of one and two cannot have side effects, so it is unimportant what order
they are declared in. In other languages, you might say that the variable two is created after the
variable one, but in Haskell that is irrelevant — the two variables are not ordered in any way,
and are just evaluated when their values are needed.
In addition to providing where blocks which can be attached to declarations,
Haskell provides let .. in blocks that together form an expression. For example, we could rewrite
the example above as follows:
integer =
let one = 1
two = 2 (1)
in one + two (2)| 1 | The variable bindings are once more aligned. The identifiers one and two must start
at the same column in order to be part of the same let block. |
| 2 | We need the in keyword after the bindings. The indentation does not matter; it can even be on
the previous line. |
let is used when you are creating an expression, and where is used when you have a declaration
you can attach the where to; other than that, the meaning of these two blocks is almost identical.
Both let and where blocks allow for type declarations, so the following code would also be
valid:
integer1 =
let one :: Int
one = 1 in
one + 3
integer2 = one + 3
where
one :: Int
one = 1Defining Functions
In Haskell, functions are defined exactly like the numbers and strings we’ve already seen, with a few bits of syntactic sugar to make it easier. For instance, a function that adds one to an integer can be written as follows:
addOne :: Int -> Int (1)
addOne =
\int -> (2)
int + 1 (3)| 1 | The type of a function that takes a single argument of type a and returns a value of type b
is written as a -> b. Thus, since addOne takes an Int and returns an Int, the type of
addOne is Int -> Int. |
| 2 | Anonymous functions are written as \argument -> expression. The backslash is the beginning of
the anonymous function (of the lambda), and the arrow -> separates the argument from the return
value. |
| 3 | The expression to the right of the -> arrow can use the arguments. In this case, since int
is the argument, and the return value is int + 1, this function returns an integer one greater
than the integer it was given as an argument. |
However, writing all functions as anonymous functions would be very tedious. To avoid this, you can simply put the argument to the function on the left hand side of the equal sign, yielding the following cleaner code:
addOne :: Int -> Int (1)
addOne int = int + 1A complete program using function declarations of this style follows:
module Main where
timesThree :: Int -> Int
timesThree x = x * 3
sayHello :: String -> String
sayHello target = "Hello, " ++ target ++ "!" (1)
main = print (timesThree 3, sayHello "World")| 1 | The only unfamiliar thing in this program should be the ++ operator. The ++ operator has
type String -> String -> String, and can be used to concatenate two strings. For example, "a" ++
"b" is equal to "ab". |
Functions of Multiple Arguments
In Haskell, all functions are single-argument functions. Every function takes one argument and returns one value. However, we can still emulate multi-argument functions! For example, consider the following function, which adds two numbers:
add :: Int -> (Int -> Int) (1)
add =
\first ->
\second -> (2)
first + second| 1 | The input to add is a single number, an Int. The output is function of type Int -> Int,
which is a function that takes a second number (also an Int) and returns some Int output (their
sum). |
| 2 | The output of the first anonymous function is a second anonymous function. The output of the
second anonymous function uses arguments to both levels of functions (first and second). |
When we pass an Int to add, we get back another function. If we pass another Int to that
function, we get the sum of the two integers as a result:
func :: Int -> Int
func = add 1
three :: Int
three = func 2In this regard, Haskell’s single-argument functions allow us to easily emulate multi-argument functions. In order to make this easier, Haskell provides us with syntactic sugar for these anonymous function declarations, just like it does for single-argument functions. Thus, we can write the function and it’s use as follows:
add :: Int -> Int -> Int (1)
add first second = first + second (2)
three :: Int
three = add 1 2 (3)| 1 | We don’t need parentheses around the output Int -> Int; those are implied. Another way of
saying this is that the -> operator is right-associative. |
| 2 | In this code, we’ve replaced the two anonymous functions with a single declaration. However, the
meaning is unchanged. We can still write add 1 :: Int -> Int and store that into a variable,
applying it to the second argument somewhere else in the code (or not at all). The process of
supplying less than the full set of arguments to a function and getting back a function expecting
the rest of the arguments is called currying, and is used very frequently in Haskell. |
| 3 | We don’t need the parentheses around add 1, as they are implied. Function application is
left-associative, meaning that elements are grouped on the left. For example, the expression a b c
d is interpreted as ((a b) c) d. |
Pattern Matching and Branching
Using simple operators such as + and * is all well and good, but most real-world functions
involve a lot of decision-making and branching based on the values they are passed as arguments. In
Haskell, this decision-making can take a number of forms.
The most common form is known as pattern matching. Pattern matching allows you to test whether your data conforms to some sort of fixed pattern in its values or structure, and execute different code depending on the pattern it matches. For example, in the following classic example, we pattern match on the argument to determine what to do:
fib :: Int -> Int (1)
fib 0 = 1 (2)
fib 1 = 1
fib n = fib (n - 1) + fib (n - 2) (3)| 1 | Always remember to include a type declaration for all your top-level values and functions! |
| 2 | In this piece of our declaration, we’ve replaced the argument to fib with a literal pattern.
If the argument to fib is equal to 0, then this part of the declaration is executed. Otherwise, it
passes through to the next declaration. This is somewhat like a switch statement in some
imperative languages, with the caveat that exactly one of the branches is taken. |
| 3 | The last declaration uses a variable n as the pattern. When you see a variable in a pattern,
it will match anything, and bind the value that it matched to that variable. Thus, it resembles
the function declarations we saw earlier. |
Pattern matching works on things besides numeric literals as well, such as strings, characters, and tuples, as demonstrated by the following ridiculous function:
match :: Int -> String -> (Int, (Int, String)) -> Int
match 0 "Hello" (1, (2, "No")) = 300 (1)
match k "x" (1, (2, "No")) = k (2)
match 0 "x" (2, _) = 500 (3)
match _ _ _ = -1| 1 | We can pattern match on several arguments at once. |
| 2 | We bind k to the value of the first argument. |
| 3 | An underscore _ is used to match any pattern and ignore its value. |
In addition to pattern matching in the function declaration, Haskell provides the case .. of
statement for pattern matching:
cases :: (Int, Int) -> String
cases tuple =
case tuple of (1)
(0, 0) -> "Nones"
(1, 1) -> "Ones"
(1, _) -> "First one"
_ -> "Other"| 1 | The specific indentation follows the Haskell layout rules. The case often appears on the same
line as the function declaration, but the beginnings of the different cases must be indented past
the case and aligned. |
In addition to pattern matching (which tests for structure equality), Haskell provides function guards for deciding between different pieces of a function declaration. For example, a comparison function could be written like this:
comparison :: Int -> Int -> String
comparison a b (1)
| a < b = "Less" (2)
| a > b = "Greater"
| otherwise = "Equal" (3)| 1 | Instead of immediately declaring the result, divide it into several cases, each prefixed by |. |
| 2 | Each case starts with |, followed by a condition (an expression of type Bool), then the rest
of the declaration. |
| 3 | The otherwise keyword is used for the fall-through default case. |
Finally, if none of these styles match what you want to do, Haskell provides a conventional if ..
then .. else statement. Since the result of this statement is an expression, the then and else
must both be present, and the results must have the same type (otherwise the entire if would not
be well-typed). Thus, the comparison function could also be written using if statements:
comparison :: Int -> Int -> String
comparison a b =
if a < b
then "Less"
else
if a > b
then "Greater"
else "Equal"The Haskell if statement is much closer to the ternary ?: operator from C-style languages than
it is to the traditional if statements found in most languages.
You’ve now been introduced to most of the various control structures that Haskell provides. The control structures provided are fairly simple; there is no looping or object-orientation. There are a few more advanced language features we will look at in the future (type-classes, list comprehensions), but the ones here are more than enough to get you started. In the next section, we’ll take a break from control structures and look at creating and using our own custom data types.
Declaring and Creating Data Types
Haskell shines in creating and managing structured data. The most common way to create a new data
type is using the data keyword:
data MyType = Constructor IntThis declares a new type named MyType. MyType is a type, like Int or String (not a value,
so you cannot write something like value = MyType.) It also creates a single function
Constructor of type Int -> MyType; these functions are commonly called constructors.
However, be careful — they are not like constructors in Java or C++; they do not do any
initialization or processing. In the case above, we only have one constructor named Constructor,
and it holds an Int. Thus, the simple type MyType is just a wrapper that holds an Int value.
We can create values of type MyType, pattern match on them, and deconstruct them to get the Int
out of them:
module MyType(main) where
data MyType = Constructor Int
deriving Show (1)
makeValue :: Int -> MyType
makeValue integer = Constructor integer
incValue :: MyType -> MyType
incValue (Constructor integer) = Constructor (integer + 1) (2)
main = print value2 (3)
where
value1 = makeValue 3
value2 = incValue value1| 1 | Don’t worry about the deriving Show just yet. We need this in order to be able to output the
data structure as a String, which allows us to use print. |
| 2 | We pattern match on the Constructor constructor. This allows us to extract the Int from the
MyType and bind it to integer, which we then use to create a new MyType. |
| 3 | If we didn’t have deriving Show, this print would result in a type error. |
Sum and Product Types
The data keyword is quite versatile. For example, constructors can have multiple arguments. Like
before, the types of the arguments are spelled out in the data declaration:
data SecondType = SecondType Int String CharIn this declaration, we’ve created a type called SecondType. It has one constructor, also called
SecondType, which takes an integer, a string, and a character. The use of this multi-argument
constructor and type is very similar to the single-argument case:
module SecondType(main) where
data SecondType = SecondType Int String Char
makeValue :: Int -> MyType
makeValue integer = SecondType integer "Hello!" 'X'
main = case makeValue 3 of (1)
SecondType _ string _ -> print string| 1 | We can use case statements to pattern match on our constructors. In this case, we only have
one pattern, and we just use it to extract the String from the SecondType value. |
The data keyword also allows you to create types with multiple constructors. Each constructor
requires its own set of constituent types. If you’ve worked with C or C++, you can think of
multi-constructor types as a sort of well-typed union. In order to create multiple constructors, you
delimit the constructors with a vertical bar |:
data Third = Third1 Int | Third2 String | Third3 Char CharThis type (called Third) has three constructors, Third1, Third2, and Third3. They take an
integer, a string, and two characters, respectively.
We can create values of type Third in three different ways, and we can pattern match on
multi-constructor data types to find out which constructor was used:
module Third(main) where
data Third = Third1 Int | Third2 String | Third3 Char Char
value1 :: Third
value1 = Third 3
value2 :: Third
value2 = Third2 "Hello"
value3 :: Third
value3 = Third3 'A' 'B'
main = case value3 of
Third1 _ -> print "Integer"
Third2 string -> print string
Third3 c1 c2 -> print [c1, c2] (1)| 1 | A string is just a list of characters, so the value [c1, c2] is just a string made up of the
two constituent characters c1 and c2. We will discuss lists in more depth soon! |
Parametric and Recursive Types
Some types, such as our hypothetical Letter or Digit types, store a fixed type and amount of
data (in this case, one letter and one digit). However, sometimes we need to store different types
of data, or different amounts of data.
In order to store different types of data, Haskell’s types are allowed to be parametric.
Parametric types are similar to various generic programming systems in imperative languages
(generics in Java, some uses of templates in C++, and so on). For example, the following type
represents a "nullable" value of some type a:
data Maybe a = Nothing | Just aThis type has one type parameter, a. The parameter is a type variable and comes
after the type name, just like an argument to a function. Like normal variables, type
variables must start with a lowercase letter or underscore.
This type also has two constructors. The first, Nothing, is similar to null, nil, or None
from other languages, and represents the absence of a value. The second constructor is just a
wrapper around a value of type a, and represents the fact that a value does exist.
We can make values of this type like this:
-- Can work for any type 'a', so we leave it unspecified.
nothing :: Maybe a
nothing = Nothing
something :: Maybe Int
something = Just 3
nothingInSomething :: Maybe (Maybe Int)
nothingInSomething = Just NothingUsing type parameters, we can create types that represent abstract ideas and data structures, such as nullable values, lists, or trees.
Note that in order to make the most of these data structures, you will sometimes need to create recursive data structures. For example, a binary tree can be represented as follows:
data BinaryTree a = Leaf a | Branch a (BinaryTree a) (BinaryTree a)This tree has a value of type a at every node. Each node is either a Leaf (in which case it is a
terminal node) or a Branch (in which case it has two subtrees). However, note that the subtrees
are also of type BinaryTree a. This type is recursive, as each binary tree can store yet another
binary tree, which allows for trees of arbitrary depth. We will deal with a similar data structure
extensively towards the end of this guide.
Other Ways of Making Types
In a typical Haskell application, some types will be large, with multiple branches separated by |
and multiple constituents in each branch. However, many types will be small wrappers around existing
types, just meant to be used for type safety. For example, in order to prevent someone from adding
together an age and a weight, you might want to create separate data types for each:
data Age = Age Float
data Weight = Weight FloatIf we write 1.0 + 2.0, the compiler will produce 3.0, regardless of what the 1.0 and 2.0
were meant to represent. However, if we try to write Age 1.0 + Weight 2.0, we will get a type
error, because the operation we are trying to do is meaningless. In order to facilitate simple
wrapper types like Age and Weight, Haskell provides the newtype keyword:
newtype Age = Age Float
newtype Weight = Weight FloatA newtype declaration is identical to a simple data declaration. However, there can only be one
constructor with one constituent type in it, which enforces the fact that newtype types are just
wrappers. In exchange for this restriction, the compiler guarantees that there will be no runtime
cost associated with using a newtype — unlike data, the constructors and de-constructors are
guaranteed to be optimized away by the compiler.
Now that you’ve familiarized yourself with data types in Haskell, read through the following short application that deals with managing a list of people:
module People(main) where
-- Wrappers for numerical types.
newtype Age = Age Float
newtype Weight = Weight Float
deriving Show (1)
newtype Address = Address String
-- A data type representing a person.
-- A person is either an adult, or a child.
-- Children must have a parent.
-- Their address is the same as their parent's.
data Person = Adult Age Weight Address
| Child Age Weight Person
-- A small set of people.
charlie, victoria, john :: Person (2)
charlie = Adult (Age 50) (Weight 150) (Address "Lombard St")
victoria = Adult (Age 52) (Weight 180) (Address "Deuce Ave")
john = Child (Age 10) (Weight 90) charlie
-- Extract the weight from a Person value.
getWeight :: Person -> Weight
getWeight (Adult _ w _) = w
getWeight (Child _ w _) = w
-- Print all the weights.
main =
print (getWeight charlie, getWeight john, getWeight victoria)| 1 | newtype declarations need deriving Show in order to be printed, just like data. |
| 2 | When declaring multiple values of the same type, you can put them in the same type declaration. Only do this if the values are intricately related and it makes sense to declare them together. |
This small program does a lot! However, we can shorten it and make it a bit clearer using record
types. Take a look at getWeight in the program above: this is effectively boilerplate. We extract
the same field from each constructor, causing us to duplicate code for every constructor we have.
Also, if we wanted to manipulate age and address, we’d have to write a function that looked more or
less identical for each of those fields. Instead of writing these ourselves, we can give the
constituent types of each constructor a name, and let Haskell generate these functions for us.
Using record notation, we could rewrite the data declaration as follows:
data Person = Adult {
age :: Age,
weight :: Weight,
address :: Address (1)
} | Child {
age :: Age,
weight :: Weight,
parent :: Person (2)
}| 1 | The fields address and parent are both partial, meaning that if you try to get the
address of a Child or the parent of an Adult, you’ll get an error. Partial functions will
be discussed more extensively later! |
| 2 | An additional benefit of this is that the code is much more self-documenting. We no longer need
a comment to tell us that the Person in the Child constructor is the parent, as we’ve given each
field of the record an informative name. |
To use our new functionality, we can simply get rid of getWeight and replace with just weight:
main = print (weight charlie, weight john, weight victoria)We can still pattern match on records and create new values in the same way we did before. However, we can also pattern match on fields themselves. We could write the following function to retrieve a person’s location:
location :: Person -> Address
location Adult{address = addr} = addr (1)
location Child{parent = adult} = location adult| 1 | To pattern match on a record, write the constructor name (Adult) followed by fields in braces.
The field name goes to the left of the =, and the variable or pattern you’d like to bind it to
goes on the right. |
We can use a similar syntax for creating new records. For example, we could define charlie as
follows:
charlie :: Person
charlie = Adult {
age = Age 50,
weight = Weight 50,
address = Address "Lombard St"
}This is a little bit more verbose, but can be clearer for complex data types and will not break if you add more data types somewhere in the middle of the product type.
Lists
At this point, we can begin looking at some real-world applications and uses of Haskell. In this section, we’ll go through one of the most basic data structures used in functional programming - the linked list.
Linked Lists
A linked list is a list in which each element is stored in its own node. Each node also has a pointer or reference to the next node in the list.
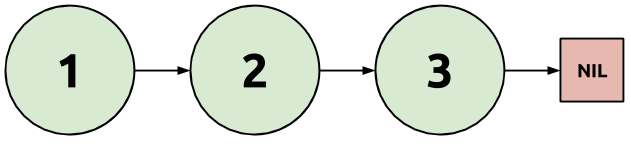
The diagram above shows a linked list with three nodes. The first node contains a one and a link to the second node. The second node contains a two, and a link to the third node. The third node contains a three, and a link to the fourth and last node. The fourth node is a special symbol "Nil" indicating the end of the list. (An empty list would be represented as just the symbol "Nil").
We could encode a recursive data structure like this one in Haskell as follows:
data List a = Nil (1)
| Node a (List a) (2)| 1 | The ending symbol (and empty list) is a single no-argument constructor called "Nil". |
| 2 | Each node has a value (the a) and a link to the remainder of the list (the List a). The a
is called the head and the List a is called the tail of the list. |
We could then create the list containing 1, 2, and 3 as follows:
elements :: List Int
elements = Node 1 (Node 2 (Node 3 Nil))However, because linked lists are so common in functional programming, Haskell has special syntax
for lists. Instead of Nil, you write [] (the empty list). Instead of Node value next, you
write value : next, with : acting as an infix data constructor. In addition, lists of known
elements can be written naturally with the elements inside square brackets, separated by commas. The list
of the numbers 1, 2, 3 would just be written [1, 2, 3]. Instead of List a, the type of a
list of a values is [a]. All of the following options are valid and semantically identical:
elements :: [Int]
elements = [1, 2, 3]
elements :: [Int]
elements = 1 : 2 : 3 : []
elements :: [Int]
elements = 1 : [2, 3]For the case of numbers, you can also write [x..y] to create a list of integers from
x going to y. For example, the list of all integers between one and ten can be written as
[1..10]. The notation [x, x'..y] indicates a list of values starting at x, incrementing by x'
- x, and going until y. For example, all even numbers up to 10 can be written as [0, 2..10]:
toTen :: Int
toTen = [0..10]
evensToTen :: Int
evensToTen = [0, 2..10]
oddsToTen :: Int
oddsToTen = [1, 3..10]Pattern Matching on Lists
In order to work with lists, we use pattern matching, like with most data structures. For example, we can use pattern matching to extract the head and tail of a list:
head :: [a] -> a
head (x:xs) = x (1)
head [] = error "empty list" (2)
tail :: [a] -> [a] (3)
tail (x:xs) = xs
tail [] = error "empty list"| 1 | The pattern x:xs mirrors the way lists are created. x is bound to the head (first element), and xs is
bound to the tail (the remainder of the list). |
| 2 | We can’t take the head of an empty list, since it has no first element. error is a special
function which throws an exception and crashes the program. So make sure you don’t take the head
of an empty list! |
| 3 | Note the type signature — we take and return a list. Like head, tail throws an exception
on an empty list. |
We can also do somewhat more advanced pattern matching. For example, suppose we have a two-element
list [1, 2] and we want to compute the sum of the two elements. Here are two ways we could do that:
list :: [Int]
list = [1, 2]
sum1 = a + b
where
[a, b] = list (1)
sum2 = a + b
where
a:b:_ = list (2)| 1 | Patterns that use square brackets require that the list be of length exactly two. A three-element list
would cause a pattern-match failure. (To match on a three-element list, you would use a pattern like
[a, b, c].) |
| 2 | In this case, we use an underscore _ to ignore everything past the second element. In a three
or more element list, everything beyond the second element would just be ignored. If we wanted to
match only two-element lists, we could write a:b:[] instead of a:b:_. |
Higher-Order List Processing
Next, we’ll take a look at some of the fundamental operations available on lists. These are the bread and butter of functional programming; as you continue with Haskell, you’ll encounter these functions on a daily basis.
Suppose you declare a list of integers:
ints :: [Int]
ints = [1..5]We’d like to perform two steps:
-
Take the square of every integer, and get a list of squares.
-
Compute the sum of all these squares.
We’ll handle each of these steps in order.
Map
In order to take the square of every integer, we’ll define the following function, which maps a function over every element of a list:
map :: (a -> b) (1)
-> [a] (2)
-> [b] (3)| 1 | As the first argument, map takes a function that transforms an a into a b. |
| 2 | As the second argument, map takes a list of a s. |
| 3 | map applies the function to every element of the list and outputs the list of resulting b s. |
Functions like these are known as higher-order functions. (Some languages also
call these types of functions "functors", but Haskell uses the word "functor"
to mean something completely different.) A higher-order function is a function takes a function as
an argument (like map, which has another function as its first argument) or returns a function as
the result. All Haskell multi-argument functions return functions as results (due to currying), so
most of the time the term higher-order function refers to functions which take other functions as
arguments.
In a standard imperative language, you might use a for or while loop to implement this map
function. However, Haskell doesn’t have loops, and instead you must use recursion in cases like
these. When beginning to write functions, break them up into separate declarations for the different
input they may receive. In this case, start by considering what map must do if it gets an empty
list as the second argument:
map f [] = []Clearly, since there are no a 's to process, the output cannot have any b 's, so map must return
an empty list.
The alternative to an empty list is one which has something in it. In that case, we pattern match on the head and the tail of the list:
map f (x:xs) = f x : map f xsTo convert the x (of type a) to type b, we apply f (of type a -> b), yielding f x (of
type b). Then, since we want to construct a list of b 's, we apply map to the remainder of the list. We
conjoin these two pieces into one list using the cons operator, :. Thus, the entire function with
our desired usage can be written as:
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs
ints :: [Int]
ints = [1..5]
squares :: [Int]
squares = map (^2) ints (1)| 1 | The (^2) syntax is a special syntax for using operators as functions. Whenever you have a
binary operator, you can put it in parentheses in order to turn it into a function. If you just put
it in parentheses, like (^), it will become a binary function; however, you can put a value on the
left or right side of the operator in order to pre-supply that value and create a unary function. In
this case, (^2) is equivalent to the anonymous function \x -> x^2. |
Folds
Now that we’ve computed the squares of our integers, we want to compute the sum. We can do this
through a left-fold (also called reduce in some languages). The idea behind folds is that we start
of with some value, and then add each element of the list to that value. The value acts like an
accumulator which can be updated as we scan through the list. A left fold (foldl) scans through
the list starting from the left, while a right fold scans starting from the right.
For our purposes, implementing a left fold will suffice. The left fold is called foldl and has the
following type signature:
foldl :: (a -> b -> a) (1)
-> a (2)
-> [b] (3)
-> a (4)| 1 | The first argument to foldl is the combining or updating function. |
| 2 | The second argument is the starting value. In order to update the value with a new element from the list, we use the first argument, which is a combining function. We pass it the current value of the accumulator and the list element, and it returns the new value of the accumulator. |
| 3 | The third and last argument to foldl is the list to fold over. |
| 4 | The output is the final accumulated value, having factored in updates for each of the elements
in the list of b values. |
As before, we should start by considering what happens with an empty list. If we get a starting value and an empty list, we have no elements that we need to process, so we should just return the starting value:
-- Return starting value when given no elements in list.
foldl _ starting [] = startingNow, suppose the list is non-empty. In that case, we pattern match using x:xs to match the head
and tail of the list. We can use the combining function with the starting value that foldl was
passed in order to create an updated value. Then we recurse on the tail of the list, passing the
updated value as the new "starting" value!
foldl f starting (x:xs) =
let newStarting = f starting x in
foldl f newStarting xsWith this left fold function, we can easily implement a function to take the sum of a list:
sum :: [Int] -> Int
sum integers = foldl (+) 0 integers (1)| 1 | In this usage of foldl, we begin with a starting value of zero. Then, our updating or
combining function is just (+). (+) is equivalent to \a b -> a + b; it takes two values and
adds them. In this case, the first value it takes is the growing accumulator, and the second value
is the list element. When it’s done, foldl returns the last accumulator value, which in this case
will be the sum of the integers passed to sum. |
With that, we can present the final program. Note that map, foldl, and sum are all defined in the
standard library and imported by default, so we explicitly hide them from the scope:
module SquareAndSum(main) where
-- Hide symbols we're redefining.
import Prelude hiding (map, foldl, sum)
-- Apply a function to every element of a list.
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs
-- Fold an accumulating operation on a list from the left.
foldl :: (a -> b -> a) -> a -> [b] -> a
foldl _ a [] = a
foldl f a (x:xs) = foldl f (f a x) xs
-- Sum a list of integers.
sum :: [Int] -> Int
sum = foldl (+) 0 (1)
ints :: [Int]
ints = [1..5]
squares :: [Int]
squares = map (^2) ints
total :: Int
total = sum squares
main = print total| 1 | According to its type signature, sum takes a [Int]. However, the
declaration seems to take no arguments! This is because we are using currying — we are supplying
foldl with only two of the three arguments it requires. Thus, when sum is passed the [Int], it
just gets passed as the third argument to foldl. |
Beware of using foldl in practice. Due to laziness, foldl builds up a lot of
unevaluated computations, and can thus take up a very large amount of memory for modestly sized
inputs. In practice, instead of foldl, use foldl' from the Data.List module.
|
There are many more useful list operations, and foldl and map are among the most important.
Implementing many of the other common list operations make good exercises in recursion and list
processing!
Laziness
Haskell, unlike almost all languages in common use, is lazy. Alternatively, one might say that Haskell has a lazy evaluation strategy, also known as call-by-need. The alternative (which applies to most other languages) is known as eager evaluation.
Lazy vs Eager Evaluation
In a lazy language, expressions are not evaluated until their value is needed. For example, consider the following code:
print (f x (y + z))In an eager language, the expression y + z will be evaluated first. All variables already store
fully evaluated values, so nothing needs to be done for f or x (besides fetching their values).
Then, f will be called with the values of x and y + z as arguments. f will compute some
result, which is then passed to the print function to be written to the screen.
Most eager languages will have some sort of consistent ordering strategy; in Python, for example, arguments to a function are evaluated from left to right. In a lazy language, we have no guarantees about what order things will be evaluated in. Instead, the order of evaluation depends on when and if the value of an expression is needed.
Consider once more our example:
print (f x (y + z))This example is a single expression which calls the print function with some argument. The entire
expression will be unevaluated until execution of the program reaches the print function. Since
the print function requires its argument’s value to format its output, the argument will be
evaluated.
Before the expression f x (y + z) can be evaluated, the value of f must be known. Unlike an
eager language, where you know every variable stores a fully computed value, a variable in a lazy
language may store a value that has yet to be computed. (These unevaluated values are often known
as thunks.)
For example, suppose that f and x were defined like this:
let x = 100 + 200
f = if x > 200
then \a b -> a + b (1)
else \a b -> a * b| 1 | Recall that \a b -> a + b is an anonymous function which takes two arguments and returns their
sum. |
To evaluate f x (y + z) we must first evaluate f. In evaluating f, we see that the value of
f depends on a condition in an if statement which depends on the value of x. Once we see that
we need to evaluate x, we pause evaluating f and take a detour to find the value of x. Once
x is evaluated (to a value of 300), the if statement can be evaluated, and f will be evaluated
to \a b -> a + b.
This value is then effectively substituted into our original expression, turning f x (y + z) into
(\a b -> a + b) x (y + z). We then simplify this by applying the anonymous function to its
arguments, yielding x + (y + z). In order to compute this final result, we must go back and make
sure that x, y, and z are evaluated. We know that x has already been evaluated, since we
needed it to evaluate f. Thus, y and z are evaluated next, and finally the entire expression
is evaluated. Once the value of the expression is known, the print function can use the value to
format its output and write it to the screen.
This cartoon is of course not exactly what happens when Haskell code is run; however, it is fairly close. In an eager language, all expressions are evaluated as soon as they are encountered. In a lazy language, expressions are only evaluated when their results are needed.
Lazy evaluation can be quite confusing to work with and reason about, especially for programmers who are used to eagerly-evaluated languages. However, lazy languages permit some very elegant algorithms, abstractions, and data structures, which truly make laziness worthwhile. (Haskell is lazy by default; there are ways to enforce order of evaluation and use eager evaluation. These are often useful for optimization of memory usage or runtime. We’ll talk more about these functionalities later.)
Inspecting Lazy Evaluation
In order to build some intuition about laziness and lazy data structures, let’s fire up GHCi. GHCi
is a Haskell interpreter which lets you enter expressions and let statements in an interactive
REPL. Enter the following code into GHCi:
let total = sum [1..1000000] (1)| 1 | Note that there is no in keyword. This is due to some syntax we have yet to talk about. For
the time being, view this as a peculiar quirk of GHCi. |
You may notice that when you enter this line, it evaluates instantaneously, with practically no
delay. This is because nothing has been evaluated yet — as far as Haskell is concerned, it knows
that total means sum [1..1000000], but it has not actually evaluated that sum yet.
We can force Haskell to evaluate total by doing something with it:
print totalYou’ll notice that it took quite a while for it to evaluate that statement. Before being able to
print the value, it had to sum up a list of a million numbers. Try entering print total again — you’ll notice that it runs much faster, now that total has been evaluated.
You can inspect the underlying structure of a variable using the GHCi :sprint directive. For
example, if you run
:sprint total
you should see that total has been evaluated to a large integer value. However, you can see
unevaluated expressions as well:
let ints = [1..10]
:sprint intsThis should output
ints = _
which simply means that the value of ints has not been evaluated yet.
Try showing the first element of ints by typing head ints into GHCi. Once you do this, the first
value will be evaluated. You can examine which bits of ints have been evaluated:
head ints -- Will show 1
:sprint intsThis should yield the string ints = 1 : _. This means that ints is a list — recall that the :
is an infix data constructor that takes a value on the left and a list on the right, and is used for
constructing linked lists. In this case, the first value is 1, but the rest of the list is
unevaluated. In order to evaluate a few more elements, you can use the take function, which takes
elements from the front of a list:
take 3 ints -- Will show [1, 2, 3]
:sprint intsNow, :sprint should yield
ints = 1 : 2 : 3 : _
which again means that the first three elements are 1, 2, and 3, and the rest of the list hasn’t been evaluated.
Finally, if we print ints, using :sprint should show you that the entire list has been
evaluated:
ints = [1, 2, 3, 4, 5, 6, 7, 7, 9, 10]
Infinite Lists
One of the strangest consequences of laziness is that our data structures are no longer restricted by the amount of memory we have, as long as we never evaluate and hold in memory the entire data structure! In fact, we can very easily have infinite lists:
let integers = 1 : map (+1) integers (1)| 1 | The value of integers (on the right hand side) depends on integers itself. In most
programming languages, this is illegal, because integers isn’t defined yet — however, in Haskell,
this is just a recursive binding which generates an infinite list. |
When encountering expressions like these, think about what would happen if they were evaluated. In
this case, consider the expression take 3 integers, which gets the first three elements of this
list. First, you would compute head integers to get the very first element. According to our
definition 1 : map (+1) integers, the first element is just 1. Next, we would get the second
element. The second element is the head of the tail. Since the tail is map (+1) integers,
the second element is head (map (+1) integers). As we saw before, map applies the function
(+1) to every element of integers. We have already computed that the first element of integers
is 1, so the first element of map (+1) integers must be 2. We can compute the third element of
integers in exactly the same way, and find that take 3 integers is just [1, 2, 3].
You can use :sprint along the way to look at how much of integers has actually been evaluated.
Finally, try evaluating the following code:
print integersYou should find that GHCi tries to print an infinite list, dumping output to the screen until you interrupt it (which you can do with Ctrl-C).
Exercises
1. Reimplement the following functions without looking at the previous code:
-- Return the first element of a list.
head :: [a] -> a
-- Drop the first element, return all others.
tail :: [a] -> [a]
-- Apply a function to all elements.
-- Return a list with the results.
map :: (a -> b) -> [a] -> [b]Remember that when you want to signal an error (such as using head on an
empty list) you can use the following function:
error :: String -> aThis function is already provided by the standard library — you do not need to (and cannot!) write it yourself.
Also, make sure you hide the standard library versions of these functions via
import Prelude hiding (map, head, tail)Otherwise, you will get errors when testing your code, because the compiler will not know which version of the function you meant.
2. In Haskell, in addition to defining your own functions, you can define your own binary operators. This functionality is used very often by library authors, and you’ll often see unusual operators being used in Haskell code. These operators definitions look like the following example:
-- Strange demo operator!
-- 11 <<!>> 10 == 21
(<<!>>) :: Int -> Int -> Int
-- Set the fixity of this operator.
-- 'r' stands for 'right-associative'
-- There's also 'infixl' for left associative operators and
-- just 'infix' for non-associative operators.
-- The digit is the precedence, and must be between 0 and 9 inclusive,
-- where 9 binds most tightly and 0 least tightly. (Function application has precedence 10).
infixr 3 <<!>>
x <<!>> y =
if x > y
then x + y
else x - yTo keep with the spirit of Haskell, let’s start off by defining two of our own operators:
-- Define your own list indexing operator.
(!!) :: [a] -> Int -> a
-- Define a list concatenation operator.
(++) :: [a] -> [a] -> [a]As before, remember to hide the Prelude version of those operators via an import statement:
import Prelude hiding ((!!), (++))3. Implement the following functions without looking at any code in this guide. Do not forget to
hide the Prelude versions, as in the previous exercises.
-- Return the first few elements of a list.
-- The integer says how many elements to return. It must be non-negative.
take :: Int -> [a] -> [a]
-- Repeat an element an infinite number of times.
-- Remember that since Haskell is lazy, as long as you don't evaluate the entire list,
-- it won't take forever! Infinite data structures are common and very useful.
repeat :: a -> [a]
-- Compute the length of a list.
length :: [a] -> Int
-- "Fold" over a list. This function is a bit complicated; you may have seen it
-- called 'reduce'. It takes three arguments:
-- 1. A function which aggregates results.
-- 2. A starting value (before aggregation).
-- 3. A list over which to aggregate the results.
-- For instance, to sum all the elements of a list, you can write:
-- add x y = x + y
-- foldl add 0 myList -- Sum all elements in myList
-- To multiply all the elements of a list, you can write:
-- mul x y = x * y
-- foldl mul 1 myList -- Multiply all elements in myList
foldl :: (a -> b -> a) -> a -> [b] -> a4. Implement the following functions:
-- Check whether an integer exists in a list of integers.
elem :: [Int] -> Int -> Bool
-- Perform a fold from the right.
-- This is like foldl, except it goes from the right instead of the left.
foldr :: (a -> b -> b) -> b -> [a] -> b
-- Return a list after dropping a few elements from the front.
drop :: [a] -> Int -> [a]
-- Repeat a list multiple times. The integer dictates how many copies you want.
-- Return the conjoined list.
replicate :: Int -> [a] -> [a]
-- Convert from two lists into a single list of tuples.
zip :: [a] -> [b] -> [(a, b)]5. Design a binary tree data structure BinaryTree a to hold elements of type a at the leaves.
This binary tree should hold values only at the leaves, and should not hold any values at the
branch nodes. Then, implement the following functions on your data type:
-- Apply a function to each value in a binary tree.
treeMap :: (a -> b) -> BinaryTree a -> BinaryTree b
-- Convert a binary tree into a list.
treeToList :: BinaryTree a -> [a]
-- Sum up all integers in a tree.
treeSum :: BinaryTree Int -> Int6. Consider the following binary tree data structure which holds values only at branches:
data BinaryTree a = Leaf | Branch a (BinaryTree a) (BinaryTree a)
deriving ShowThis exercise has no coding part — instead, try to understand the following code snippet. The
function replaceWithMin aims to replace every value in a binary tree with the minimum value in the
entire binary tree. While most languages would require two passes over the tree to do this (one
pass to find the minimum and one pass to replace it), we can use properties of lazy evaluation to do
this in one pass:
-- Replace the value at each branch with
-- the minimum of all values in the tree.
-- Leaves are assumed to hold the value 0.
replaceWithMin :: BinaryTree Int -> BinaryTree Int
replaceWithMin tree = tree'
where
-- Find the minimum value and replace values in the tree with it.
(tree', minValue) = go tree
-- Return the modified tree and the minimum value of the old tree.
go :: BinaryTree Int -> (BinaryTree Int, Int)
-- Base case: Leaves are assumed to hold value zero.
go Leaf = (Leaf, 0)
-- Recursive case - a branch
go (Branch value left right) =
let -- Find minimums of left and right branches.
(left', leftMin) = go left
(right', rightMin) = go right
-- Replace value with minimum value.
newTree = Branch minValue left' right'
-- Find the minimum of this subtree.
subtreeMin = minimum [value, leftMin, rightMin]
in (newTree, subtreeMin)We could use it like this:
example :: BinaryTree Int
example =
Branch 3 Leaf
(Branch (-1)
(Branch 5 Leaf (Branch 10 Leaf Leaf))
(Branch (-3) Leaf (Branch 7 Leaf Leaf)))
example' :: BinaryTree Int
example' = replaceWithMin example
main :: IO ()
main = print exampleThe output will be something like this, module formatting:
Branch (-3) Leaf
(Branch (-3)
(Branch (-3) Leaf (Branch (-3) Leaf Leaf))
(Branch (-3) Leaf (Branch (-3) Leaf Leaf)))
As extra practice, modify this function to work on the binary tree data structure you designed earlier (which has a value at each leaf but no values at the branches).