In this notebook, we'll look at finger trees, a general purpose functional data structure developed in the paper by Hinze and Paterson. Finger trees provide a functional sequence data structure, which provides amortized constant-time access and appending to the front and end of the sequence, as well as logarithmic time concatenation and random access. In addition to good asymptotic runtime bounds, the data structure turns out to be incredibly flexible: when combined with monoidal tags on the elements, finger trees may be used to implement efficient random-access sequences, ordered sequences, interval trees, and priority queues.

Please note that all of the algorithms in this notebook are effectively sourced from the paper linked above; some of the images are also from the paper. I highly recommend reading the paper itself, before or after this guide.

Developing the Data Structure

The basis and motivation for finger trees comes from 2-3 trees. 2-3 trees are trees which can have two or three branches at each internal node and which have all of their leaves at the same level. While a binary tree of uniform depth $d$ must have $2^d$ leaves, 2-3 trees are much more flexible, and may be used to store any number of elements (the number does not have to be a power of two).

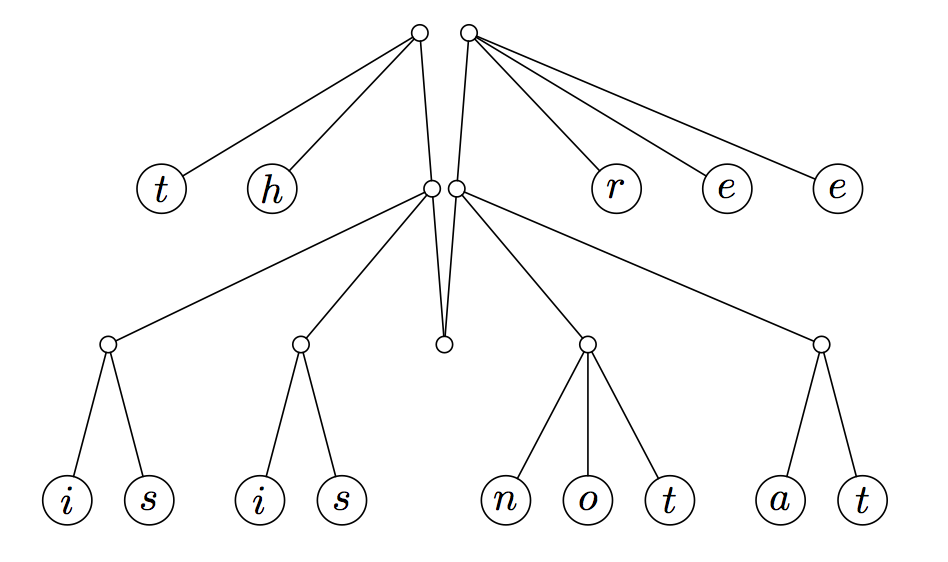
Consider the following 2-3 tree (image taken from the original finger-tree paper linked above):

This tree stores fourteen elements. Access to any of them requires three steps, and if we were to add more elements, the number of steps for each one would grow logarithmically. We would like to use these trees in order to model sequences. However, in many application sequences are very often accessed repeatedly at the front or back, and much less often in the middle. To accomodate this use case, we can modify this data structure to prioritize front and back access over other features.

In our case, we add two fingers. A finger is simply a point at which you can access part of a data structure; in imperative languages, this would simply be a pointer. In our case, though, we restructure the entire tree and make the parents of the first and last children the two roots of our tree. Visually, consider taking the tree above, grabbing the first and last nodes on the previous-to-last layer, and pulling them up, letting the rest of the tree hang down:

This new data structure is known as a finger tree. The finger tree is composed of several layers (boxed in blue below) which sit along its spine (the brown line):

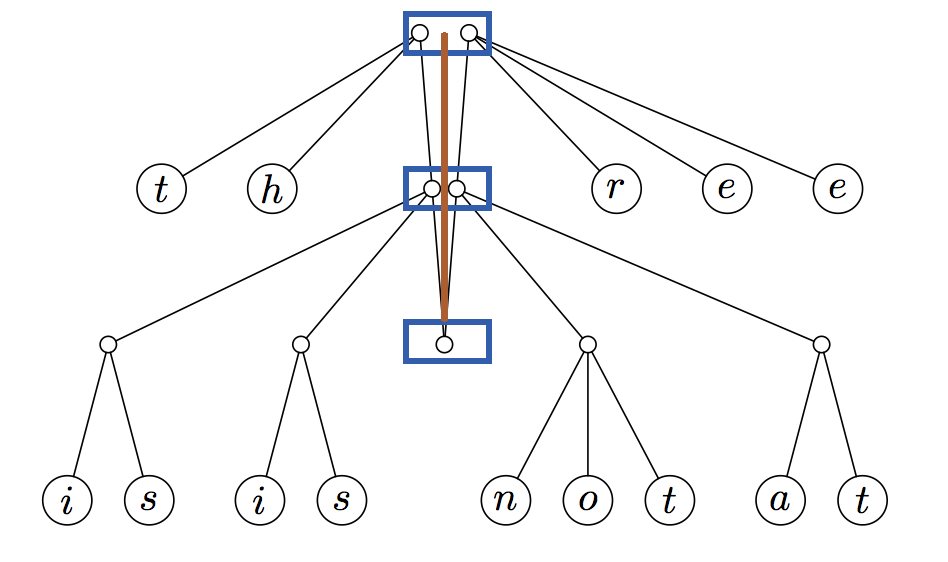
Each layer of the finger tree has a prefix (on the left) and a suffix (on the right), as well as a link further down the spine. The prefix and suffix contain values in the finger tree – on the first level, they contain values (2-3 trees of depth 0); on the second level, they contain 2-3 trees of depth 1; on the third level, they contain 2-3 trees of depth 2, and so on. This somewhat unusual property comes from the fact that the original 2-3 tree was of uniform depth. The edges of the original 2-3 tree are now at the top of the spine. The root of the 2-3 tree is now the very bottom element of the spine. As we go down the spine, we are traversing from the leaves to the root of the original 2-3 tree; as we go closer to the root, the prefix and suffixes contain deeper and deeper subtrees of the original 2-3 tree.

With this description out of the way, let's go ahead and define this data structure. First, we must define the 2-3 tree structure which will be used to store things hanging off the spine:

Note that the node is parameterized by what type its child is. This allows nested nodes to be used to represent 2-3 trees, giving us a guarantee of uniform depth. For example, a 2-3 tree of depth 1 could be just aNode Char:

However, we can also create deeper 2-3 trees. For example, a 2-3 tree of depth 2 could be a Node (Node Char):

Note that this representation guarantees that 2-3 trees have uniform depth, because the depth is represented in the type of the tree. This has its own disadvantages (it's harder to write functions that are parametric over the depth of a tree), but will work well in our case.

For later convenience, let's implement some utilities which let us treat Node values as lists of length two or three. This uses the OverloadedLists extension for GHC, which allows you to implement fromList and toList for different data types and then use pattern matching on them as if they were lists:

Now that we have our 2-3 tree type, we need a type to store the prefix and suffixes that hang off the finger tree spine. If our finger tree is exactly analogous to a 2-3 tree, then the very first prefixes and suffixes can have either 2 or 3 elements, and intermediate ones can only have 1 or 2 (because one of the links goes up to the higher level in the spine). However, for the sake of uniformity, this requirement is relaxed for finger trees, and instead each prefix and suffix holds between 1 and 4 elements. (It must be 1, 2, 3, or 4 – no other values are allowed.) Although we could store the prefix and suffix in a list, we will instead devise a custom constructor that can only store the right number of elements:

Working with these affixes is going to be somewhat tedious, so we'll quickly define some helper functions that treat these affixes as lists:

Now that we've defined the data types necessary for storing values (the 2-3 tree storing the values and the affixes attached to the spine), we can create the spine data structure. This data structure is what we call the finger tree, and we define it as follows:

In the definition above, the deeper field of a FingerTree a has type FingerTree (Node a). This means that the values stored at the next level are 2-3 trees that are one level deeper. Thus, the affixes in the first layer of a FingerTree Char will just store Chars; the second layer will be a FingerTree (Node Char) and will have affixes that hold 2-3 trees of depth 1 (Node Char); the third layer will be a FingerTree (Node (Node Char)) and will have affixes that store 2-3 trees of depth 2 (Node (Node Char)).

Now that we've defined our finger tree data structure, spend a little bit longer staring at the example tree from before, making sure that you understand how to translate that tree into a FingerTree Char:

The translation of this tree is as follows:

Finger Trees as Sequences

The motivating reason behind developing our strange finger tree data structure was to have a sequence-like tree which could be accessed quickly at the front and back. Thus, in this section we implement operations that view finger trees as sequences.

Prepend and Append

Let's begin by appending an element to the front of a finger tree. Ideally, we could prepend an element simply by prepending it to the prefix of the tree. While this would work for finger trees that have one, two, or three elements in their prefix, it would not work on a finger tree that has four elements in its prefix. In that case, we would be unable to add one more element to the prefix, because the prefix cannot have a length greater than four. To avoid a prefix of length five, we instead take three of these five elements, turn them into a Node using the Branch3 construction, and then prepend them to the deeper finger tree:

We can do the exact same thing for appending on the right, since we have access to the right end of the tree in the same way as the left end:

We can now construct finger trees easily by appending and pre-pending elements to them:

Although we've implemented append and prepend for finger trees, it may seem like we haven't gained much in terms of efficiency over trees, because if we get unlucky and the tree already has a lot of prefixes of length four, we may have to traverse all the way down the tree to add the elements. As a result, the worst case of any prepend or append operation is $O(\lg n)$, where $n$ is the number of elements in the list.

While the worst case hasn't gotten better, performance for the typical use case has imporoved. In most uses of prepend and append, the user will be appending or prepending many elements in a row, each time only keeping the new modified tree and discarding the old tree. To analyze this use case, assume that we are performing $m$ append or $m$ prepend operations in a row.

To analyze the asymptotic runtime of this use case, note first that all the non-recursive branches of append are constant time. If the original tree is small (Empty or Single x), or if we can immediately add the element by modifying the prefix, the append or prepend is takes $O(1)$ time. The recursive case (where the affix has length four) is the problematic one. However, when we encounter an affix of length four and want to add to it, we immediately rebalance the tree such that the affix has length two. Thus, we know for sure that the next operation that wants to add an element to that affix can do so immediately in constant time, and will not need to descend another level. From this we can deduce that no more than half the operations could possibly need to recurse down into the second layer of the finger tree; for each operation that does recurse, there must be at least one operation that doesn't. Since the same logic applies to the finger tree at the second layer, we know that only one quarter of operations could possibly go down to the third layer. Continuing with the same logic, the $n$th layer of the finger tree could only be visited by one out of every $2^{n-1}$ operations. Thus, the total time $T$ for all $m$ of the append or prepend operations is at worst going to be

$$T = m + \frac{1}{2}m + \frac{1}{4}m + \frac{1}{8}m + \cdots,$$

because $m$ operations do something at the first level of the tree, $\frac{1}{2}m$ operations do something at the second level of the tree, and so on. However, even if we assume there are an infinite number of layers (and clearly there are less), this series of terms sums to $2m$ (which you can compute using the formula for the sum of a geometric series). Thus, we take $O(m)$ time for $m$ operations, so while the worst case for a single operations is $O(\lg n)$ with $n$ elements in the tree, the amortized time for this use case is just $O(1)$ for each prepend or append.

Views (First and Last)

In the previous section, we implemented an append (|>) and a prepend (<|) operation to add elements to the start or end of our finger-tree-based sequence. However, in addition to adding elements, we need to be able to look at them and remove them. Both of these operations will be based on a more fundamental view operation, which we implement next.

The view operation has two versions: a left view viewl and a right view viewr. Each of these takes one element off the end of the finger tree (left and right end, respectively) and returns that element along with a finger tree representing the rest of the elements. To make this clearer, an equivalent of viewl for a list would be

A naive implementation of viewl for finger trees might look as follows:

We can even test that this implementation works for an empty tree and for the example tree we devised before:

While it may seem that it works, this implementation actually has a very serious flaw. Can you spot it?

The following code block demonstrates this issue:

When we wrote the case of viewl that dealt with Deep constructors, we simply took an element off the left prefix. While we know this works and this will indeed yield the first element, the finger tree that contains the rest of the elements may not be valid. In the block above, we tried to use viewl to create a finger tree that contained zero elements in its prefix, which of course is illegal and immediately raised an error.

In order to handle this case, we have to explicitly check for the number of elements in the finger tree prefix. Then, if there is only one element, we cannot remove it; instead, we must use viewl on the deeper finger tree to get a Node a. This Node a will contain two or three more values, so we can remove the single element in the prefix and instead replace the prefix with the contents of the Node a, thus maintaining the invariant that every affix has between one and four elements. The following code implements viewl properly, reusing the same View a data structure from before:

With this new implementation of viewl, our failing test from before works fine:

The right equivalent of viewl, viewr, is implemented in almost exactly the same way, substituting uses of the prefix for the suffix and vice versa:

We use it just like we use viewl, and it gives us access to the end of the sequence:

Since we now have our view primitives, we can easily implement a few other functions, such as the finger tree equivalents of head, tail, last, init, and null:

In particular, we can now easily convert between lists and finger trees:

Using finger trees is now even simpler:

Concatenation

Another operation we can easily implement using the finger tree data structure is concatenation. The operations we currently have are enough to implement simple concatenation, since we can recursively view and then append elements. A very simple implementation of concatentation follows:

Although this implementation works fine (as you can verify by looking at the value of something like exampleTree >< exampleTree), it's fairly slow. In terms of asymptotic runtime, it's the same as using toList to get a list of the finger tree elements, concatenating the lists, and then using fromList to convert back to a finger tree. We've shown that |> takes amortized $O(1)$ time, but we must do that $O(m)$ times, where $m$ is the number of elements in the right tree passed to ><. Thus, the total running time is $O(m)$ – it's linear in the number of elements we're appending.

It turns out we can do much better by utilizing the structure of the finger tree. Before doing this, though, we're going to need a helper function called nodes, which can convert from a list of items to a list of Nodes of items:

For every two elements in the original list, nodes will output only one element in the new list of nodes. In order to accommodate odd numbers of elements, nodes will emit a Branch3 when it is left with a triple. As a result, we know for sure that if nodes is given a list of $n$ elements, it will emit a list of $\lfloor \frac{n}{2} \rfloor$ nodes. This will be important later on.

Next, we're going to redefine concatenation in terms of a somewhat strange operator we'll call concatWithMiddle. concatWithMiddle takes two FingerTree a values to concat, as well as a list of elements to stick between the two trees. Implementing >< with concatWithMiddle is trivial – we just pass an empty list as the extra elements:

The only thing remaining to implement is concatWithMiddle. We need a few special cases to deal with the Empty and Single constructors; in these cases, concatenation simply reduces to $O(1)$ appends. We handle the list of extra elements in the middle by also using several appends or prepends.

In addition to the edge cases, we must handle the common case in which both trees are created with the Deep constructor. When this is the case, we also return a Deep constructor with:

• prefix equal to the prefix of the left tree
• suffix equal to the suffix of the right tree
• deeper (the next finger tree) equal to a recursive call to concatWithMiddle

We also must handle the suffix of the left tree and prefix of the right tree. These can be combined with the middle elements and passed to concatWithMiddle. Since the deeper finger tree stores Node a values instead of a values, we use our helper function nodes to create a list of Nodes we can pass to the recursive concatWithMiddle call. This may be somewhat confusing, and should be elucidated by reading the code:

We can test that this code works as we did before, by looking at the output of something like exampleTree >< exampleTree:

While it's clear that this code is functional (no pun intended), it's not clear that we've actually done any better in terms of asymptotic runtime guarantees. If we look at the base case for concatWithMiddle, we're still doing a ton of prepends! Since every time we recurse down another layer, we add elements to the middle list (from the unused affixes), is it possible that we still have something like $O(m)$ prepends done in the base cases?

Surprisingly enough, the answer to this is no. We can prove that the base cases still take only $O(1)$ amortized time. The magic here lies in our use of nodes. As we showed when we defined nodes, nodes is guaranteed to output a list no more than half the length of the input list. Using this property, we can easily track the maximum length that the middle list can be at any point in the computation.

When the computation starts, we know that the middle list has length zero, since we pass concatWithMiddle an empty list in our definition of ><. At each step, we add two affixes (a suffix and a prefix) to the middle list before applying nodes to it. We know that the affixes have no more than four elements, so we are adding at most eight elements to the middle list. As a result, after we apply nodes, our list can have no more than eight elements, because as we add more and more elements, the length of the output of nodes can get closer and closer to eight; however, it cannot go above eight, because if we start out with less than or equal to eight elements, add eight elements, then divide the length by two, we will end up with less than or equal to eight elements again. To convince yourself, you can trace through an example execution in which you start with zero elements and add eight at each recursive step:

• Step 0: Middle list has 0 elements.
• Step 1: Add 8 elements (4 from suffix, 4 from prefix). nodes reduces the length by half, so middle list now has 4 elements.
• Step 2: Add 8 elements, for a total of 12; nodes reduces length to 6.
• Step 3: Add 8 elements, for a total of 14; nodes reduces length to 7.
• Step 4: Add 8 elements, for a total of 15; nodes reduces length to 7.

Note how the last two steps both yielded a list of the same size – once the computation reaches that point, the middle list will not become any longer as the recursion continues. Thus, the length of the middle list is bounded by seven, which is $O(1)$ (a constant); as a result, we can confidently say that all of the base cases are also $O(1)$ amortized running time, because they do no more than eight prepends.

Since the base cases are all constant time, the main contributor to the runtime of our >< is the recursion. At each recursive step, we look at the deeper tree in both the left and right trees passed to concatWithMiddle; we reach a base case as soon as one of these trees is not created with the Deeper constructor. The depth of these trees grows logarithmically with the number of elements in them; if the finger tree has $n$ elements, it's depth is $O(\lg n)$. Since our runtime is proportional to the minimum depth of either tree, our asympotic runtime bounds are $O(\min(\lg n, \lg m)) = O(\lg(\min(m, n)))$, where $n$ and $m$ are the number of elements in the left and right trees, respectively.

Applications of Finger Trees

We've described the finger tree data structure and figured out how to use it as a sequence, at least as far as access to the front and back of the sequence are concerned. However, we have yet to figure out how to access any element of the sequence without traversing a ton of elements to get to it.

Instead of just defining a random access primitive that operates on finger trees, we will instead define a more general search operation. We'll then use our general search operation to implement random access sequences and prioritiy queues, both based on finger trees.

To implement our search operation, we will need each node of the finger tree to be marked with an annotation. To that end, we begin by redefining our finger tree data structures to store annotations at each branch:

We require that these annotations are monoidal; that is, that the type v is a member of the Monoid typeclass. Recall that a monoid is something that has an associative append operation (<>) with an identity (empty). This is embodied in the following typeclass, which is slightly different from the Monoid typeclass that ships in the Haskell base library:

We also require that the annotations are not arbitrary annotations, but are actually related to the values in the tree. The annotations must be measures of elements of the tree. More precisely, there must be a measure function that accepts an element of the tree and outputs an annotation for that element. To create that function, we must implement the following Measured typeclass for our element type and annotation type:

We can implement a measure for all the data types used in our finger tree – FingerTree, Node, and Affix. For FingerTree's Deep constructor and Node, we cache the annotations, so we just need to retrieve them when we implement measure. For the Empty and Single constructors, we must use the identity element empty and the measure function:

For Affix, we have chosen (somewhat arbitrarily) to not cache the annotations in the Affix data structure, so instead our implementation of measure computes it from the values in the affix:

The definition above is why we require that annotations be a monoid. Since the annotations form a monoid, we can easily compute annotations for branches and affixes based on the measures of the values they contain. The measure of a branch or an affix is the monoidal sum (concat) of all the measures of the values they contain.

In order to simplify our lives, we also need to provide convenience constructors for our new Node constructors and the Deep constructor. First, we implement the IsList typeclass for Node values, so we can easily create new nodes without worrying about annotations:

Next, we provide a convenience constructor for trees made with the Deep constructor. This constructor takes care of setting the annotation, and thus has a Measured constraint. However, this constructor also differs from Deep in that it allows the prefixes to be empty, which will greatly simplify our code later. In order to use the constructor, we're going to have to change a lot of our older code to handle the new FingerTree v a type; in the following code block, pay attention to deep and the functions that it uses, but ignore the reimplementations of View, viewr, and viewl – they are just the same code you saw earlier with a little bit more logic to handle the annotations:

We've gone through a whole lot of setup without anything interesting; however, at this point, we're finally prepared to work on our search algorithm, which we will later use to implement random access into our finger trees (as well as other things). Our search will accept a predicate (v -> Bool) that operates on our monoidal annotations (v). The predicate (let's call it pred) must satisfy a few properties:

• pred empty == False: The predicate must return False on the monoidal identity element.
• If pred x == True, then pred (x <> y) must also be True, regardless of y. This means that pred is monotonically increasing, and adding more elements to the monoidal sum must not make it false.

The search will scan through our finger tree, adding up the annotations of all the elements as it goes. It will check whether each of the sums satisfies our predicate pred. The search will find and return the location in the finger tree sequence where pred switches from being False to True; if no such place exists, the search will fail.

The goal of our search is depicted in the following graphic from the paper by Hinze and Paterson:

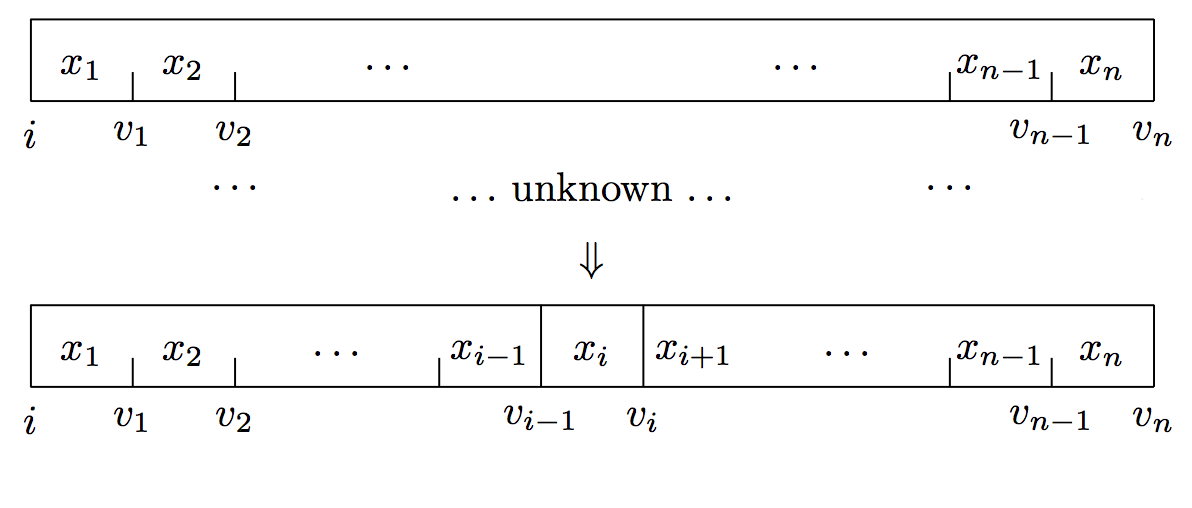
In the graphic above, $v_x$ is the sum of annotations for elements $0$ through $x$, which is why the $v_x$ values appear on the space between the elements. The very first value, $v_0$, is the monoidal identity element empty, depicted there as $i$. The search locates the element $x_i$ such that pred applied to $v_{i-1}$ is False and pred applied to $v_i$ is True.

For example, the following function splitList implements this search algorithm on simple lists, returning a tuple where the first element contains $x_0$ through $x_{i-1}$, and the second element contains $x_i$ and all later elements:

For lists, the implementation of splitList is fairly straightforward. The implementation for finger trees, which we will call split, shares the same idea, but ends up being somewhat more convoluted to implement. We define a custom Split data structure to store the split location that our search found; our upcoming split function will return a Split as its result. In this Split data structure, the left and right parts of the sequence are stored as finger trees, and the element $x_i$ (which caused pred to switch) is stored directly:

Finally, we can implement split. split is the workhorse of our search. Given a subsequence (passed in as a FingerTree v a) and the annotation at the start of the subsequence, split returns a Split indicating where the predicate switches. Of course, split assumes that the predicate applied to the left value is False – if not, then the search is pointless, as the predicate should return true for all points in the subsequence.

If you look carefully at the definition of split, you'll note that it does a constant amount of work at each step. (splitList is a constant amount of work, because we only pass it lists made of nodes and affixes, which cannot exceed four elements in size.) Each step also recurses deeper if it needs to (if the split is in the deeper tree and not in an affix). Thus, in the worst case, we'll do $O(1)$ work for each of the layers of the finger tree; since there are $O(\lg n)$ layers in the finger tree, the split operation has worst case runtime bounds of $O(\lg n)$.

With that, we've completed split and implemented the bulk of the functionality necessary to use finger trees as random access sequences. In the next section, we'll look at exactly how we can use these monoidal annotations to do random access.

Random-Access Sequences

We're prepared to get to the meat of our random access algorithm. In order to implement random-access trees, we're going to annotate each subtree with the number of elements it contains. To achieve this, we just need to annotate each leaf with the value 1 and use summation as monoidal addition. Since our finger trees automatically take care of their own annotations, all we need to do is specify the types the finger tree stores, the measure of those types, and how to combine subtree sizes (just addition):

Using the types and instances above, leaves of our finger tree are annotated with the value one. Intermediate nodes are annotated with the size of their subtree. In order to find the $n$th node in our sequence, we can look for the place where the sum of the annotations becomes greater than $n$. For example, if we search for the place where the annotations become greater than five, the split point we find will be at the sixth element, because the sixth element is what makes the annotations become greater than five. In a zero-indexed sequence, five is indeed the index of the sixth element!

Thus, the implementation of random access sequences requires a very simple (!) operator, which is just a thin wrapper around split:

Let's create an example sequence to test our algorithm on:

We can test our indexing works by attempting to index into the sequence using each of the possible indices. We should recover the list of elements in the tree:

To use this in a serious library, you would want to wrap this in another layer which checks that the index is non-negative and in bounds, and only perform the search if it is, return a Nothing on failure and a Just result on success. In the current implementation, we ignore failure, and if we try to access an element that doesn't exist, the search crashes with an exception that would be rather confusing to the end user:

Priority Queues

In addition to random-access sequences, we can easily use the same data structure and the same search algorithm for implementing efficient functional priority queues. We will assume that a priority queue is a data structure PriorityQueue a with the two functions push :: PriorityQueue a -> a -> Int -> PriorityQueue a (which pushes a value of a given integer priority onto the queue) and pop :: PriorityQueue a -> (a, PriorityQueue a) (which takes the maximum priority element, removes it from the priority queue, and returns a tuple with the element and the new tree).

In order to implement our priority queue, we must just choose a different monoid. Instead of our finger trees storing Values and being annotated with Sizes, they will store Prioritized items and be annotated with Prioritys:

We must then implement the Measured typeclass, which in turn requires us to implement Monoid for our Priority type. As we will see, our monoid cannot operate on integers alone – it will need a minimum priority, which we call NegativeInfinity:

As with our random-access sequences, the Measured typeclass is pretty simple to implement. In this case, the measure of any Prioritized item is simply a Priority representing its priority:

With these instances, we can define a priority queue data structure as a finger tree:

Implementing push is easy: just add an element to the sequence. It doesn't matter how you add it, so we'll just use a prepend:

In order to implement pop, we'll need to use our Monoid instance, along with our split routine. Since our monoid instance combines priorities by choosing the largest one, each subtree will be annotated with the largest priority it contains. Thus, to find the maximum priority p in the entire tree, we can just measure the tree itself, since it will be annotated with the largest priority it contains. Then, to find an item of a priority p, we can just search for where the predicate == Priority p becomes true.

Recall that we had two requirements on our predicate: first, it must be false on our identity element empty, and second, it must be monotonic – once it is satisfied, it will remain satisfied if we add in all the other elements of the sequence. Both of these properties hold in this case. Since empty is defined to be NegativeInfinity, we know that checking for equality with some priority will return false. The second property is true by virtue of the fact that the priority we're searching for, p, is known to be the maximum priority that exists in the tree; thus, no matter how many elements we add to the monoidal sum, we know the result will just be Priority p, because the monoidal sum picks out the largest priority (which we know is p).

Thus, we can implement pop as follows:

Let's now test our priority queue. We'll add in several strings prioritized by their length, and verify that our priority queue will return the longest ones first:

Conclusion

Finger trees, as described by Hinze and Paterson, are a pretty awesome data structure. They provide amortized constant time append and prepend (assuming a use case of repeated appends and prepends), amortized constant time left and right views, and logarithmic time concatenation. They can be parameterized by a monoidal annotation; then, given a monotonic boolean predicate on the monoidal annotations, a search can be performed in logarithmic time to determine which element (if any) tipped the scales and caused the incremental monoidal sum along the sequence to pass the predicate. This very general search algorithm allows very high code reuse – by changing the type stored by the finger tree and adding two typeclass instances, finger trees can be used as very different data structures. In this guide, we used finger trees to implement random-access functional sequences and priority queues with push and pop. In the original paper, they also describe several other data structures and operations, including ordered sequences (with access and insert) and interval trees. Due to the efficiency and asymptotic guarantees provided by finger trees, they are the basis for the sequences provided in the Haskell base library under the Data.Sequence module.

This guide is written as an IHaskell notebook. If you would like to work with it interactively, you may download it as a notebook.