This is the fourth of several blog posts meant to serve as a crash course in Haskell for someone already familiar with programming and somewhat familiar with functional programming. The previous post in the series was here.
What is Abstraction?
A key feature of programming languages is their capability for designing abstractions. Most imperative languages support functions, and you may be familiar with a few that support more advanced abstractions, such as macros in Lisp or classes in most popular modern languages.
Though languages will have some abstractions as language features, abstractions are occasionally encoded as social constructs, often called "design patterns". Although they aren’t a fundamental part of programming language, things such as factories (common in Java), visitor patterns, thread pools, and client-server request-response communication protocols are all design patterns just as much as functions or classes.
In mathematics, abstraction takes on a slightly different meaning. Abstract mathematics relies on defining simple objects and a few axioms that relate them, and seeing what sort of results these axioms yield. (An axiom is simply a fact taken for granted, something that is assumed to be true without proof.) For instance, an important mathematical abstraction is the group:
Mathematical abstractions have a tendency to be very general, and can be hard to apply to real-world scenarios and data. With the example above, how could we use a group structure in our software? Without a more concrete application, that abstraction is hard to utilize. On the other hand, traditional abstractions in software are straight-forward to apply, but can be hard to analyze rigorously. We get very few theoretical guarantees simply by knowing that some class implements the visitor pattern.
While the standard style of abstractions can be used in Haskell (and often are), we often prefer to use more rigorously defined mathematical abstractions. We represent these abstracts through a typeclass along with a set of laws that well-behaved instances must obey. (The language does not and cannot verify that the laws are followed, so whenever you write an instance of a typeclass with a set of associated laws, it is up to you to verify that the laws hold. The community tends to quickly point out invalid instances if they are in published libraries.)
The group abstraction above might be defined as the following typeclass:
-- A group has...
class Group g where
-- an identity element,
identity :: g
-- an addition operation,
add :: g -> g -> g
-- and an inverse for each element.
inverse :: g -> gWhenever we wrote an instance for this class, we would want to verify that the following laws hold:
-- Our addition is associative.
forall x y z. x `add` (y `add` z) == (x `add` y) `add` z
-- We have a two-sided identity.
forall x. identity `add` x == x
forall x. x `add` identity == x
-- Every element has an inverse.
forall x. inverse x `add` x == identity
forall x. x `add` inverse x == identityThe laws above are not valid Haskell, but are just a way to express the laws that relate to our Group typeclass.
The abstraction of a group turns out not to be very useful in Haskell, so we won’t spend any more time on it; it’s served us well as an example, and is no longer useful to us. Note that although that particular abstraction isn’t useful, the style in which we defined it (as a typeclass with some laws) is common throughout the Haskell ecosystem. With that in mind, let’s spend the rest of this guide looking at some useful abstractions that Haskell programmers use every day.
Monoids
The first abstraction we’d look to look at is fairly similar to the Group example, but
somewhat more restricted. Like before, we’d like to generalize a notion of combining
different elements using some sort of addition. For instance, we can combine numbers using
+ and we can combine lists and String s using ++. However, while numbers
have inverses (so we could make them a Group), there’s certainly no notion of an inverse
for strings or lists. To simplify our life, we can get rid of the requirement for an inverse.
The resulting algebraic structure is called a monoid:
This definition is similar to the definition of a group; all we’ve done is removed one requirement! The typeclass looks pretty familiar, too:
-- A monoid has...
class Monoid m where
-- an identity element,
mempty :: m
-- and an addition operation.
mappend :: m -> m -> mAs usual, this abstraction comes with a set of laws, corresponding to the items in the mathematical
definition above. We use the operator <>, which is just an infix alias for mappend.
-- Our addition is associative.
forall x y z. x <> (y <> z) == (x <> y) <> z
-- We have a two-sided identity.
forall x. mempty <> x == x
forall x. x <> mempty == xThe value of the monoid abstraction comes from its wide applicability, so let’s take a look at some examples. The most obvious instance would be one for numbers:
-- Numbers form a monoid under addition.
instance Num a => Monoid a where
mempty = 0
mappend = (+)This instance, while tempting, has a number of problems (no pun intended). The main semantic one is that that’s not the only way to define a monoid over numbers! For example, we could also try to define something like this:
-- Numbers form a monoid under multiplication as well!
instance Num a => Monoid a where
mempty = 1
mappend = (*)The other slightly more technical issue with both of the instances above is that they create an
opportunity to seriously confuse the Haskell type system. If you try to define these instances,
you’ll get an error message complaining about UndecidableInstances.
In order to solve both of these issues, we can wrap the number in a semantically-meaningful
newtype.
We’ll create two new types – one called Sum for the monoid under addition, and another
called Product for the monoid under multiplication.
-- Numbers form a monoid under addition.
newtype Sum a = Sum a
instance Num a => Monoid (Sum a) where
mempty = Sum 0
mappend (Sum x) (Sum y) = Sum $ x + y
-- Numbers form a monoid under multiplication.
newtype Product a = Product a
instance Num a => Monoid (Product a) where
mempty = Product 1
mappend (Product x) (Product y) = Product $ x * yWith instances like these, we can write a general "sum" function to combine a list of monoids.
-- Combine a list of monoid elements into one.
mconcat :: Monoid m => [m] -> m
mconcat = foldl' mappend memptyWe can use this as a sum or a product by wrapping our values in the Sum or Product
constructor:
sum :: Num a -> [a] -> a
sum nums = s
where Sum s = mconcat $ map Sum nums
product :: Num a -> [a] -> a
product nums = p
where Product p = mconcat $ map Product numsThe pattern of using newtype s to distinguish between monoids is fairly common, because for
many data types there are multiple ways to interpret them as a monoid. For instance, for the
Bool type we can interpret the binary operation <> as either an "and" or an "or",
which yield the All and Any monoids, respectively:
newtype All = All Bool
instance Monoid All where
mempty = All True
mappend (All x) (All y) = All $ x && y
newtype Any = All Bool
instance Monoid Any where
mempty = Any False
mappend (Any x) (All y) = All $ x || yThe all and any functions can then be implemented very similarly to the
sum and product functions above.
Yet another instance of this pattern (once more, no pun intended) is the First and
Last monoids. These extract values from a list of Maybe values; as their names may
suggest, they extract the first Just values and the last Just values encountered.
newtype First a = First (Maybe a)
newtype Last a = Last (Maybe a)The instance implementation is left as an exercise to the reader. In both cases, the identity should
be Nothing. In the First case, mappend should keep the left-most Just result it
sees, whereas in the Last case, it should keep the right-most Just result.
Not all monoids fit this newtype ing pattern. For example, an incredible useful monoid instance is the
one for the Ordering data type, implemented as follows:
-- An ordering, used to compare values.
-- The Ord typeclass requires a function compare :: a -> a -> Ordering.
-- Necessary for sorting and other order-dependent operations.
data Ordering = LT | GT | EQ
-- Allow for lexicographical ordering.
instance Monoid Ordering where
mempty = EQ
mappend EQ ord = ord
mappend ord _ = ordThis monoid allows us to easily write comparator functions. For instance, suppose we had a type representing someone’s name:
data Name = Name {
first :: String,
middle :: String,
last :: String
}If we wanted to implement an ordering on names that sorted first on last names, then first names, then middle names, we could easily implement such an ordering:
instance Ord Name where
compare name1 name2 =
compare (last name1) (last name2) <>
compare (first name1) (first name2) <>
compare (middle name1) (middle name2)Recall that the function compare :: a -> a -> Ordering is necessary for implementing the
Ord typeclass, and that we already have an Ord implementation (and thus a
compare function) for String s. Using the String compare and the
Monoid instance for Ordering, we can easily write the lexicographic ordering for
our Name data type.
The last monoid we’ll look at is the [a] monoid. This instance can be constructed almost
trivially using the empty list and ++. however, this monoid has an interesting property.
Although it has a somewhat special syntax, [] is actually a type constructor (similar to
Maybe). [] takes any type a and spits out a valid Monoid. For
this reason, the list type [a] is referred to as the free monoid – we get it
for free for any type a, without any extra effort on our part. Although this is fairly
uninteresting for monoids, we’ll see later that other algebraic structures also admit free variants
which are somewhat harder to derive but can be used with great effect.
Finger Trees and Monoids
As with many things, mastery and understanding of monoids comes not only in knowing their
definitions but also in being able to use them in practice. To that end, let’s look at a Haskell
library called fingertree which utilizes the monoid abstraction to great effect. (The same
algorithms and data structures are used in Data.Sequence module from the
containers package, which implement fast random-access sequences for Haskell.)
Before looking at finger trees, let’s consider a simpler case – searching for the $n$th element in a list. Using standard Haskell lists, this takes $O(n)$ time, since you need to traverse $n - 1$ elements of the linked list to get to the $n$th element. In order to do this faster, we can superimpose a binary tree structure on top of this list:

The terminal nodes store the list elements. The intermediate nodes are annotated with the number of children they have. Thus, the top node will be annotated with the length of the list, and every leaf will be annotated with the value one.
We could write the example tree above as follows:
data Tree a = Branch Int (Tree a) (Tree a) | Leaf Int a
tree :: Tree Char
tree =
Branch 4
(Branch 2 (Leaf 1 'A') (Leaf 1 'B'))
(Branch 2 (Leaf 1 'C') (Leaf 1 'D'))If we want to quickly reach the $n$th element in this tree, instead of starting at the beginning of the list and traversing forwards, we could start at the top of the tree and look for the place where the number of children to our left is greater than $n$.
For instance, suppose we wanted to access the fourth element. We start at the top of the tree, and look at the left and right branches. Since the left branch is annotated with a two, we know that we must look to the right in order to get the fourth element, since the left branch only has two children in it. We take the right branch, and once more look to the left and to the right. This time, we’re looking at a pair of leaves, so the annotations are both one. However, we know that these correspond to indices three and four, since we know we’ve skipped two elements by going to the right branch of the top node (because the left branch had annotation two). Thus, we know that the right branch of our current node is the third element, and we can access and return it. As long as the tree we impose on top of our list is balanced, we will be able to access any element in $O(\log n)$ time.
We can implement this search fairly easily.
-- Extract the annotation from a leaf or intermediate node.
annotation :: Tree a -> Int
annotation (Branch i _ _) = i
annotation (Leaf i _) = i
-- Look up an index in the tree.
treeLookup :: Tree a -> Int -> Maybe a
treeLookup tree i =
-- Use a helper function which takes the number of elements skipped.
-- At the top-level call, we've skipped no elements, so we pass zero.
go tree 0
where
-- At a leaf, make sure the index is the one we expected.
-- If it isn't, then we reached the leaf too soon, probably because
-- the binary tree was smaller than expected (index out of bounds).
go (Leaf a x) seen =
if a + seen == i + 1
then Just x
else Nothing
-- At a branch, look at the left branch and decide whether to go there.
go (Branch _ left right) seen =
-- Only take the left branch if the index we're searching in
-- comes earlier than the right branch.
if annotation left + seen > i
then go left seen
else
-- If we take the right branch, we've skipped some elements.
-- Pass the total number of skipped elements to the recursive call.
go right (annotation left + seen)The fingertree package extends the data structure here into 2-3 finger trees, which are
similar to balanced binary but with a few properties that make them much nicer for immutable
languages. For our purposes, we simply need to know that the trees are somewhat balanced and give us
approximately $O(\log n)$ access time to their leaves, and that all the data in the trees is stored
at the leaves, just like in the example above.
However, instead of storing an integer as an annotation, the intermediate nodes are annotated with a generic monoidal tag. Thus, the tree above would be written somewhat differently:
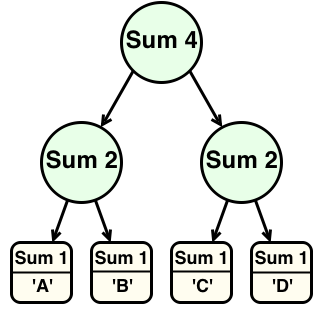
Note that the tag on any node is just the monoidal product (in this case, the sum) of any nodes it has as a child.
In order to create a new FingerTree, the package provides an empty value
representing a finger tree with no elements in it. Elements may be inserted on the left or right with the functions
(<|) :: Measured v a => a -> FingerTree v a -> FingerTree v a
(|>) :: Measured v a => FingerTree v a -> a -> FingerTree v aThe libraries suggests remembering these operators as triangles with new elements at the pointy
ends. Unlike our previous example where we manually created leaves with annotation value one, we
don’t pass the annotation directly. Instead, our value type must be an instance of the
Measured typeclass, which looks like this:
class Monoid v => Measured v a | a -> v where
-- Things that can be measured.
measure :: a -> vIgnoring the funky bar and a -> v in the class declaration (those are functional
dependencies), this class says that you can convert your value a into some measure
v which is a monoid.
This measure is the monoidal tag that gets placed in the tree. Thus, we can re-implement our
fast-lookup list as a FingerTree where the measure of any value is just Sum 1. We choose Sum 1 because we want to add (as in normal addition) the tags of the children
to get the tag of the parent, which is what the monoid instance for Sum does.
-- An element of our fast-access list.
data Element a = Element a
-- The measure of any element is just one.
instance Measured (Sum Int) (Element a) where
measure _ = Sum 1At this point, we can use functions provided in the fingertree package to implement our
search. It turns out our lookup is already mostly implemented, though not in the way we might
expect! The package provides the following functions to us:
-- Given a monotonic predicate p, dropUntil p t is the rest of t after
-- removing the largest prefix whose measure does not satisfy p.
dropUntil :: Measured v a => (v -> Bool) -> FingerTree v a -> FingerTree v aThis is a more general version of the drop function we’re used to (the one that chops off
elements from the front of a list). However, instead of chopping off a fixed number of elements,
dropUntil keeps dropping elements until their combined measure satisfies some predicate.
Recall that v is a monoid, so all the measures of the dropped elements can be combined
before being passed to the predicate p.
In order to use this to implement our lookup, we just need to create a predicate p which
returns False until some desired $k$ elements have been dropped. Since the monoid just
counts the total number of elements, this predicate can be created by thresholding on the number of
dropped elements; in other words, p = (> Sum k). The Sum monoid conveniently
implements Ord, so we don’t need to unwrap it.
Once we apply dropUntil (> Sum k), we are left with a sequence that starts with the $k$th
element. We can extract it using viewl, which looks at the leftmost element of the finger
tree; this yields a left view data structure, which we can then pattern match on to extract our
result. Thus, the complete lookup would be
index :: FingerTree (Sum Int) (Element a) -> Int -> Maybe a
index tree k =
-- Discard the first k elements, and look at the leftmost remaining element.
case viewl (dropUntil (> Sum k) tree) of
-- If it's empty, we've dropped all elements,
-- and this index was out of bounds to begin with.
EmptyL -> Nothing
Element x :< _ -> Just xWe can then use this as follows:
-- fromList is provided by Data.FingerTree
let tree = fromList (map Element ['a'..'z']) in
print (index tree 13) -- prints Just 'n'Since this application (quick lists) is so common, its shipped in base Haskell as Data.Sequence.
The real power of abstraction comes from code re-use, and it turns out that the finger tree data structure plus the monoid abstraction allow us great flexibility. With almost the same code as before, we can use the finger trees as a priority queue, instead of a fast access list. In order to do that, we must change the definition of our monoid. For demonstration purposes, our tasks (elements in the priority queue) will be strings, and the priority of a string will be its length:
data PrioritizedString = Str String
priority :: PrioritizedString -> Int
priority (Str s) = length sThis time, instead of searching for an element with a particular index, we wish to search for an
element with a particular priority. The key difference lies in the fact that instead of combining
priorities through addition, we combine priorities by taking their maximum. Before we write the
Measured instance, we must have an appropriate monoid for maximums:
data Maximum = Max Int deriving Eq
instance Monoid Maximum where
-- The identity element is just the minimum possible integer.
mempty = Max minBound
-- Combining two elements is taking the greater one.
mappend (Max x) (Max y) = Max (max x y)Once we have this monoid defined, we can define the measure for our prioritized strings:
instance Measured Maximum PrioritizedString where
measure = priorityWith these two instances in place, we’re ready to go. We’d like to be able to find the highest
priority element element in our priority queue. First of all, we know that the top node annotation
will be the monoidal sum of all annotations below it. Since our monoid just takes the maximum of two
elements to combine them, the top annotation will be the maximum priority in the tree. Thus,
to find the top priority element, we just dropUntil we reach a priority that is equal to
the one at the top of the tree:
longestString :: FingerTree Maximum PrioritizedString -> Maybe String
longestString tree =
-- The maximum priority is at the top of the tree.
let maximumPriority = measure tree in
-- Discard elements until we find the most important one.
case viewl (dropUntil (== maximumPriority) tree) of
-- If it's empty, there were no elements to begin with.
EmptyL -> Nothing
Str x :< _ -> Just xThere are two interesting things to note about this code. First of all, we use measure
directly on the tree, and we do not in any way extract its top node. This is because
Data.FingerTree provides us with the following instance:
-- The cached measure of a tree.
instance Measured v a => Measured v (FingerTree v a) where ...This instance just accesses the measure at the top level of a tree, which is exactly what we need.
The other thing you’ll note is that we use equality on the priority, which is why we needed a
deriving Eq when we originally defined our Maximum data type.
At this point, we’ve successfully used the fingertree library and data structure to define
two different things: a list with fast indexing, and a priority queue. Due to the clean interface
that the Monoid typeclass and abstraction allows, we were able to define both with not much more
than ten lines of code. We were able to leverage a very efficient and powerful library to do
multiple very different things by using the right fine-grained abstraction, learning about monoids
along the way.
Functors
In the previous section, we started off our study of abstraction in Haskell with the concept of a monoid, which was, roughly speaking, a type of thing that you can combine together. In this section, we’ll get some more practice with Haskell-style abstract thinking by discussing yet another abstraction used by Haskell programmers on a daily basis.
Recall the map function, which applies a function to every element of a list:
map :: (a -> b) -> [a] -> [b]What makes lists special, though? Suppose we had a simple binary tree data structure:
-- Binary tree with a value of type 'a' at each node of the tree.
data Tree a = Leaf a | Branch a (Tree a) (Tree a)We can define a function very similar to map for our Tree data structure. Let’s
call it treeMap:
treeMap :: (a -> b) -> Tree a -> Tree b
treeMap f (Leaf a) = Leaf (f a)
treeMap f (Branch a left right) =
Branch (f a) (treeMap f left) (treeMap f right)Indeed, we’re beginning to see a pattern! We often have a container (such as [a] or
Tree a), and we’d like to apply some function of type a -> b to every element in
the container.
What we’re looking at turns out to be a bit more abstract than just containers. In Haskell, this abstraction is known as the functor (a name which, like many things in Haskell, comes from category theory). The associated type class looks like this:
class Functor f where
fmap :: (a -> b) -> f a -> f bWe’ve already seen two types that fit this pattern, namely lists and trees. We can provide an instance of each:
-- This instance already exists in the standard library.
instance Functor [] where
fmap = map
instance Functor Tree where
fmap = treeMapNote that we’re implementing a typeclass for Tree, not Tree a. Although
Tree by itself is not a type (just something we can use to create a type, often called a
type constructor), we can use it in typeclasses. In fact, if we look at the signature of
fmap we see that it contains the types f a and f b, which means that
whatever f is, it has to be a type constructor that takes exactly one
argument.
So far, we’ve seen that we can create typeclasses that abstract over types (things like
Maybe a and Int) as well as typeclasses that abstract over type constructors (like
Maybe or Tree). Not only are these completely different things, but it would make
no sense to mix them! Suppose we tried to implement a functor instance for Int:
instance Functor Int where
fmap = ...In this case, fmap would have type fmap :: (a -> b) -> Int a -> Int b, which makes
no sense (what is an Int a?).
In order to make sure that instances and types makes sense, Haskell has a kind system, which is effectively a type system on top of types (instead of on top of values). The kind system is a bit simpler, though, having only the following two rules:
-
The kind of all value types (such as
Maybe a,Int, andString) is denoted*(an asterisk). -
The kind of a type constructor that takes something of kind
kand outputs something of kindgis denotedk -> g.
While the first rule is fairly simple, the second can be a bit more difficult to parse. Kinds with
-> act similarly to types with ->. A type with kind * -> is something
that takes a concrete value type (such as Int) and yields another concrete value type. A
good example of this would be Maybe – Maybe takes a type, such as Int,
and yields a new value type, Maybe Int. Thus, Maybe on its own must have kind
-> . By the same rules, we can determine that Either must have kind -> * -> *.
In the case of the Functor instance, we can tell by the signature
fmap :: (a -> b) -> f a -> f b that the type f must have kind * -> ,
because the type f a appears as a real value (an argument to fmap) and must thus
be of kind .
Before moving on, let’s look at a few more examples of functors to solidify our understanding. In
order to write a Functor instance, we need a type of kind * -> * (a type
constructor that takes on argument). One type constructor we’ve worked with a lot is Maybe,
and indeed, this is one of the most common functor uses in Haskell. A Maybe value
represents a value or computation that might have failed (and yielded Nothing). Coming from
an imperative language, a Maybe a may be similar to a nullable a. In order to
work with these failed or nullable values, we can use the following functor instance:
instance Functor Maybe where
-- Do nothing with a Nothing.
fmap f Nothing = Nothing
-- Apply the function to whatever is inside the Just.
fmap f (Just x) = Just (f x)It turns out that this instance is incredibly useful for chaining together computations that
work on something that might’ve failed. For instance, suppose we want to use the following
lookup function:
-- Look up a value in an association list.
lookup :: Eq a => a -> [(a, b)] -> Maybe bGiven a list like [(1, "Hello"), (2, "Bye")] we can use lookup to extract the first
b associated with a given a:
let associations = [(1, "Hello"), (2, "Bye")] in
print (lookup 1 associations) -- Prints Just "Hello"Suppose we’d like to do a lookup, and then perform some other computations if it succeeds (for
example, reverse the string and remove duplicate characters). One way to achieve this is through a
case statement, using nub from the Data.List module:
-- Lookup a string in an association list.
-- Then, reverse it, and remove duplicate consecutive characters.
case lookup 1 associations of
Nothing -> Nothing
Just string -> nub (reverse string)Alternative, using our Functor instance for Maybe, we can write this very cleanly
and succinctly with fmap:
fmap (nub . reverse) (lookup 1 associations)We create a new function by composing nub and reverse, and then apply it inside
the Maybe. Just like the case, this yields Nothing if the lookup fails,
or a Just value if it succeeds.
Just like we have an instance for Maybe, we can create one for Either. Recall that
the Either type is declared as follows:
data Either a b = Left a | Right bSince it takes two type parameters, it must be of kind *+ -> +*+ -> +*. A Functor
instance declaration for Either wouldn’t make sense, since Functor requires
something of kind *+ -> +*. However, by supplying Either with one variable in the
declaration, we can make it’s kind into *+ -> +*: just like you can curry Haskell functions,
you can curry Haskell types. Thus, we can write the following instance
instance Functor (Either a) where
fmap f (Left a) = Left a
fmap f (Right b) = Right (f b)Note that by declaring the instance for Either a, we satisfy the requirement that the
functor be something of kind * -> *. What this means is that the a is fixed
throughout the fmap, so using fmap on something of type Either a b cannot
change the a (but it can change the b). In this instance, the type of
fmap is specialized to
fmap :: (a -> b) -> Either c a -> Either c bNote that we have to change the name of the first type variable in Either a to
Either c, in order to avoid conflicts with the a and b in a -> b.
Since many Haskell data structures have more than one the parameter, the trick of currying one type
parameter and using the curried type to declare a functor is fairly common. For instance, we can do
the same thing with the tuple type (a, b): we fix the a and declare a
Functor instance with the b as the functor contents:
instance Functor ((,) a) where
fmap f (a, b) = (a, f b)Note that due to a strange quick of Haskell syntax, we write (,) a in order to declare a
tuple type constructor of kind * -> * which has the first element as a and the
second element as an argument to the constructor.
Note that a similar syntactic quirk applies to function types. Namely, in order to use the type
(c ->) of kind *+ -> +*, you must write (->) c. Thus, the type (->)
c b is completely equivalent to c -> b. The observation that (->) c has kind
*+ -> +* might lead us to an intriguing question… can we write a functor instance for
it?
Suppose we want to write a Functor instance for (->) c. We’d start with our general
instance scaffold:
instance Functor ((->) c) where
fmap = ...However, what would we do with fmap? What does that even mean?
In this case, it’s often helpful to think about the types involved, and let the types guide your
coding. We know that for a functor f, the definition tells us that fmap has type
fmap :: (a -> b) -> f a -> f b. Since we are specializing f to (->) c,
fmap must have type (a -> b) -> (->) c a -> (->) c b. If we undo the syntactic
quirkiness, we find that fmap has type (a -> b) -> (c -> a) -> (c -> b). Since
we’re letting the types guide our intuition and coding, can you think of something that has that
type? The key observation is that both of the two arguments are one-argument functions, and the
output of one is the input to the other. It turns out that the type of this fmap is the
same as the type of (.), the composition operator! Alternatively, we can write function
composition ourselves, and write the following instance:
instance Functor ((->) c) where
fmap f g = \c -> f (g c)The following instance is identical in semantics:
instance Functor ((->) c) where
fmap = (.)And that’s it – it turns out that (->) c can indeed be made into a functor, and pretty
easily, too!
This raises two questions:
-
Is this really a functor? Does it behave similarly to the other functor’s we’ve seen?
-
What does it mean that this is a functor? What’s the intuition behind this instance?
The first question can be answered by doing what we usually do with Haskell abstractions – coming up with a set of laws that instances of the abstraction must follow, and verifying that the particular instance we’re interested in follows those laws.
In the case of functors, we’d like to enforce a few of our basic intuitions. Our intuitions for
functors should tell us that fmap ing a function over a functor is equivalent to applying
the function inside the functor. Due to this intuition, we may think that if we apply a function
that does nothing, that should have no effect and do nothing to the larger data structure. We can
codify this in the following law:
fmap id == idNote that we are writing in point-free style, where we avoid mentioning the actual object that these
functions are applying to. What we really mean is that for any functor f and any type
f, if any x has type f a, fmap id x must be equal to x.
The other law is motivated in the same way. Since fmap ing a function is like applying a
function inside the container, fmap ing the composition of two functions (where one function
is directly applied to the output of another) should be the same as fmap ing the first
function and then fmap ing the second function. In other words,
fmap f . fmap g == fmap (f . g)These two laws are known together as the functor laws, and codify the behaviours that a
"proper" Functor instance must follow. These are quite useful in guiding us in instance
implementation. For example, suppose we tried to implement the following Functor instance
for lists:
instance Functor [] where
fmap _ [] = []
fmap f xs = [f (head xs)]We can verify that the type of fmap is correct. However, the behaviour is a little bit
strange – we only keep the first element of the list! Indeed, this strange functor instance would
be eliminated by checking the first functor law:
-- First functor law: fmap id == id
fmap id [1, 2, 3] /= id [1, 2, 3]
-- The first functor law is not satisfied:
-- fmap id [1, 2, 3] == [1]
-- id [1, 2, 3] == [1, 2, 3]Now that we have some functor laws to guide us, we can answer our first question and verify that our
instance for (->) c is a valid functor. Since fmap is just (.), we can
check the first law by verifying that
fmap id g == id g
-- ...which expands to...
id . g == gHowever, we know that id does nothing when composed (on the right or the left), so the
first law holds! The second law can be verified in the same manner – by taking the definitions of
fmap, expanding them, and then using what we know about function composition and id to
prove what we want.
Finally, we can answer our second question, and try to provide some intuition for this functor.
Although we can attempt to provide intuition, it is important to remember that ultimately, a
Functor is simply any type along with an implementation of fmap which satisfies
the functor laws. Our intuition may be helpful for reasoning about this functor, but the definition
is just that – something which satisfies the requirements and laws of a functor. With that
said, the intuition that helps with the (->) c functor is that we can view this as a data
structure with a hole in it, where the hole needs something of type c to fill it.
For example, suppose we have a data structure
data Thing = Thing Int StringIn that case, we can create a type that represents a Thing with a hole.
type ThingWithHole = Int -> ThingThe data structure with a hole is represented by a function, because once we get something to fill
the hole (an Int), we can create a complete data structure (a Thing). Thus,
applying fmap to something of type (->) c a is like operating on a data structure
of type a with an unfilled hole of type c, just like applying fmap to
something of type Maybe a is operating on a data structure of type a that might
actually be null (Nothing).
Monads
Functors, along with the Functor typeclass and fmap, can be very useful for
talking about computations happening inside a container or computational context. For example, we
can use the Functor instance for Maybe in order to write code which operates on a
failed computation and/or nullable value (see the previous section for some examples). But there are
many cases where the Functor abstraction turns out to be insufficient.
Consider the head function that takes the first element of a list:
head :: [a] -> a
head [] = error "empty list"
head (x:xs) = xInstead of crashing with an error on empty lists, we may instead want to signal failure by returning
a Maybe value, allowing us to write safer, typechecked code. We could rewrite head
and call it headMay, with the -May suffix indicating that it returns a
Maybe value:
headMay :: [a] -> Maybe a
headMay [] = Nothing
headMay (x:xs) = Just xNow, suppose we’re storing a 3D array as a list. (Due to the runtime characteristics of linked
lists, this is a terrible idea in practice!) For some reason, we need to access the top left
corner of this 3D array. In other words, we have a triply nested list (type []) and
we’d like to access the first a in it by repeatedly taking the head of these
lists. If we’re using plain old head, this is very easy:
firstElement :: [[[a]]] -> a
firstElement = head . head . headWe can test that it works by plugging in firstElement [[[1]]]; indeed, we get 1,
as expected. However, if we plug in [[]] or [[[]]], we get the standard
head exception, since the element we want to access doesn’t exist.
Naturally, as Haskell programmers, we’d like to rewrite this to be safe, just like we changed
head into headMay. A first attempt might look something like this:
-- Does not work!
firstElementMay = headMay . headMay . headMayHowever, if you try putting this into GHC, you’ll see that these types don’t match! By returning a
Maybe, we’ve broken our ability to compose functions! We might be tempted to turn to our
trusty Functor instance, since we’ve seen that that using fmap will help us with
error handling. If we try that, we might get something like this:
-- Typechecks, but doesn't do what we want!
firstElementMay = fmap (fmap headMay) . fmap headMay . headMayIndeed, that definition typechecks (better than nothing!), but instead of just giving us a
Maybe a we get a much uglier beast of the form Maybe (Maybe (Maybe a)). Clearly,
this is not what we wanted, because pattern matching on that thing will be a huge pain!
The underlying reason for the difficulty here is that the Functor instance is good for
modeling a single missing value, but it isn’t food for modeling a process in which any
individual step might fail. In words, one might describe what we’re doing as a process:
Take the head three times, and if any of those fail, return Nothing, otherwise, return
Just the result. Indeed, we can implement this with pattern matching:
-- Works, but is very clunky.
firstElementMay :: [[[a]] -> Maybe a
firstElementMay xs = case headMay xs of
Nothing -> Nothing
Just xs' -> case headMay xs' of
Nothing -> Nothing
Just xs'' -> xs''Eek, that’s ugly! In order to clean this up, we’re going to follow our intuition of describing this as a process that might fail at any step. Let’s implement this as the following function:
processWith :: Maybe a -> (a -> Maybe b) -> Maybe b
processWith value func =
case value of
Nothing -> Nothing
Just x -> Just (func value)We’ve named this function very deliberately: if we use it in infix form (using backticks to turn the function into an infix operator), we get something that is very element and reads almost like English:
-- Clean and working!
firstElementMay :: [[[a]] -> Maybe a
firstElementMay xs =
headMay xs `processWith` headMay `processWith` headMayNote that in the definition above, we have the first headMay as a special case. We start
off our processing chain with its result, headMay xs. In order to write the entire process
as one pipeline without the first one being a special case, we’ll define a strangely named
return function which just starts us off inside the Maybe:
return = JustNow we can write this pipeline in a uniform manner. We use return to put something inside
the pipeline, and then use processWith to define what needs to happen:
firstElementMay :: [[[a]] -> Maybe a
firstElementMay xs =
return xs `processWith` headMay
`processWith` headMay
`processWith` headMayThe name return may seem a little strange at first, but stick with it for now – it will
make sense eventually! (Note that return is just a name. Don’t make the mistake of thinking
it’s something syntactically special, just because other languages tend to have return as a
keyword!)
Using return and processWith, we can define very clean and elegant processing
pipelines. It turns out this pattern is very common in Haskell, and in programming in
general. Before formalizing this abstraction, let’s look at another example.
The key to this abstraction is that, roughly speaking, we’re generalizing over types of
computation. In the case of processWith and Maybe, we are creating a pipeline of
processes that might fail and modeling a computation that has the ability to fail at any step. At
any step, our potentially failing computation can produce either one value or zero values (failure).
We can generalize this behaviour by talking about a computation that can produce any number
of values at each step.
In order to represent the state of a computation that can produce multiple values, we’ll just use a plain old list. At each step of the computation, we’ll take all the current values, process them with the next step of the computation, and collect all the results. Note that the step gives us a list of results, as well. The result looks like this:
processWith :: [a] -> (a -> [b]) -> [b]
processWith values nextStep =
let newOutputs :: [[b]]
newOutputs = map nextStep values in
concat newOutputs(Note that this is showing another application of this pipelining abstraction; we can’t actually
write two functions named processWith with different type signatures. That’s what
typeclasses are for.)
Let’s try this with a simple example. We’ll start with the list [1, 2, 3] and then we’ll
filter it by using a function that gets rid of odd numbers, \x -> if odd x then [] else
[x]. Combining these with processWith, we get
[1, 2, 3] `processWith` \x ->
if odd x
then []
else [x]As expected, this gives us the result [2]. (While you may note that using filter
would be much simpler in this case, this simple case does show off how our pipeline works in
general.)
Let’s try this on another example. Suppose you want to write a function which takes the Cartesian
product of two lists. Namely, given lists of x s and lists of y s, it produces all
the pairs (x, y). For the lists xs = [1, 2] and ys = ["Hi", "Bye"], this
would produce the output list [(1, "Hi"), (1, "Bye"), (2, "Hi"), (2, "Bye")]. We could
write this using pattern matching, though it takes a bit of thinking to figure out how to do it
right:
cartesianProduct :: [a] -> [b] -> [(a, b)]
cartesianProduct xs [] = []
cartesianProduct [] ys = []
cartesianProduct (x:xs) ys = map tuple ys ++ cartesianProduct xs ys
where
tuple y = (x, y)Alternatively, we could model this as a process which outputs multiple values. At the first step,
the process outputs the xs; at the second step, it outputs all the ys; then, it
combines them with tuples. This might seem a bit convoluted, but produces straight-forward (if
syntactically ugly) code:
cartesianProduct :: [a] -> [b] -> [(a, b)]
cartesianProduct xs ys =
xs `processWith` (\x ->
ys `processWith` (\y ->
[(x, y)]))At this point, we can complete our pattern by implementing a return function:
return :: a -> [a]
return x = [x]Now we see why it’s called return: it has a tendency to be used when we need to output a
final value from our computation pipeline! Rewriting our Cartesian product with return is a very
minor modification:
cartesianProduct :: [a] -> [b] -> [(a, b)]
cartesianProduct xs ys =
xs `processWith` (\x ->
ys `processWith` (\y ->
return (x, y)))Although this end result is arguably simpler than our original pattern matching example, this style of programming can be very natural. For instance, we wanted to extend this to three lists, the changes would be very small:
cartesianProduct3 :: [a] -> [b] -> [c] -> [(a, b, c)]
cartesianProduct3 xs ys zs =
xs `processWith` (\x ->
ys `processWith` (\y ->
zs `processWith` (\z ->
return (x, y, z))))On the other hand, modifying the original pattern matching crossProduct may be a bit
tedious and somewhat more error-prone.
As I alluded to earlier when we redefined the meaning of processWith, this abstraction is
codified in a Haskell typeclass, as usual. Although one might want to call this typeclass something
like Pipeline or Process or Sequenceable, in Haskell this typeclass is
called Monad. The typeclass renamed processWith to an infix operator written
>>= (pronounced "bind"):
class Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m bNote how the type signature of >>= looks exactly like processWith, if you replaced
m with Maybe or [] (the list type constructor).
We can implement Monad instances for Maybe and [] using the
processWith and return definitions we saw previously:
instance Monad Maybe where
Nothing >>= _ = Nothing
Just x >>= f = f x
return = Just
instance Monad [] where
values >>= nextStep = concat (map nextStep values)
return x = []With these instances, our previous functions become
firstElementMay :: [[[a]] -> Maybe a
firstElementMay xs =
return xs >>= headMay
>>= headMay
>>= headMay
cartesianProduct :: [a] -> [b] -> [(a, b)]
cartesianProduct xs ys =
xs >>= (\x ->
ys >>= (\y ->
return (x, y)))If you’ve heard a lot about monads in Haskell, this is all they are – they are a pattern for describing these sorts of pipelines. That’s it!
Of course, like many abstractions, there are many applications of this abstraction where the word
"pipeline" or "computation" won’t seem to be quite right, which is why Haskell programmers have
a tendency to prefer abstract names (which may seem meaningless to the rest of us). As with the
Monoid abstraction and the Functor abstraction, something is a Monad if
it implements the methods in the typeclass and follows some set of laws (called, unsurprisingly, the
monad laws). It’s important to note that there are no other requirements for being a
Monad, which means that sometimes, you’ll find Monad instances for things that do
not follow your intuitions of "pipelines" at all.
Like we did with Functor s, we’ll try to motivate the monad laws with intuition about how
these pipelines should be have. So far, we’ve defined return as something hat just
wraps a value in our Monad. In the case of Maybe, we wrapped values by putting
them in a Just, while with lists, we wrapped values by putting them in a one-element list.
We’ll enforce the intuition that return doesn’t do anything except wrap values with two
laws, the first being as follows:
m >>= return == mThis says that if you process m using return, you just get m back.
The second law is effectively a reverse of the first laws. Instead of processing a value which is
already in a monad with return, we’ll lift a non-monadic value into a monad using
return. Then, we’ll process this value with some function, and verify that the result would
be the same had we just applied the function to the non-monadic value in the first place.
return x >>= f == f xThe last monad law is a little bit more difficult, but effectively states that >>= is an
associative operator.
(m >>= n) >>= p == m >>= (\x -> n x >>= p)Note that this isn’t quite associativity of >>=, since we can’t write m >>= (n >>= p)
on the right hand side (because n is a function, not a value in a monad). Monads that don’t
follow this law can be very unintuitive. This law states that the grouping of things in the
pipeline doesn’t matter; if our values go through the entire pipeline, it doesn’t matter if we view
the first two processes as one group (the left hand side of the equation above) or if we view the
second two processes as one group (the right hand side). This may seem like something we can take
for granted, but this is worth encoding as a law precisely because it seems like something we’d want
to take for granted.
While typeclasses and laws can be pretty powerful on their own, the Monad abstraction is so
important in Haskell that it has its own syntax, known as do notation. This syntax allows
us to write these monadic "pipelines" very cleanly, without resorting to anonymous functions like
we did in the cartesianProduct example. Do notation has three rules, which dictate how
do notation is expanded into a standard Haskell expression.
Expansion 1: The block of code
do
variable <- m
nextStepis expanded to
m >>= (\variable -> do
nextStep)Note that nextStep may use variable, and may consist of multiple statements.
Expansion 2: The block of code
do
firstStep
nextStepis expanded to
m >>= (\_ -> do
nextStep)This case is identical to the previous one, but no variable name is bound. The output of m
is ignored.
Expansion 3: The block of code
do
let x = y
nextStepis expanded to
let x = y in do
nextStepThis allows us to easily embed let statements in do blocks. Note that there is no
in after the let!
\end{enumerate}
With this notation, our firstElementMay and cartesianProduct functions become even
cleaner:
firstElementMay :: [[[a]] -> Maybe a
firstElementMay xs = do
first <- headMay xs
second <- headMay first
headMay second
cartesianProduct :: [a] -> [b] -> [(a, b)]
cartesianProduct xs ys = do
x <- xs
y <- ys
return (x, y)Although do notation is incredibly convenient, beware of viewing it as simple imperative
programming. Although it may look like an escape hatch from the functional paradigm into a more
standard imperative language, do notation is just syntactic sugar over
return and bind (>>=); forgetting that can lead to confusion and misunderstanding.
Also, note that there are times where using return and >>= directly may be simpler
than using do notation, so do not be afraid to use them without the syntactic sugar. (For
instance, the firstElementMay implementation is arguably cleaner without do
notation.)
Summary
So far, we’ve seen three abstractions commonly used in Haskell: the monoid, the functor, and the monad. There are a few other abstractions that we will cover at a later point, but these three will get you the majority of the way to Haskell fluency.
Recall that we started by defining a monoid as follows:
Whenever we had a mathematical abstraction that defined some set (such as the monoid $M$), we could
describe the set as a type in Haskell, and describe the abstraction on the set as a typeclass.
The resulting typeclass is (unsurprisingly) called Monoid in Haskell, and is defined as
follows:
class Monoid a where
-- Identity of 'mappend'
mempty :: a
-- An associative operation
mappend :: a -> a -> a
-- Fold a list using the monoid.
-- For most types, the default definition for 'mconcat' will be
-- used, but the function is included in the class definition so
-- that an optimized version can be provided for specific types.
mconcat :: [a] -> a
mconcat = foldr mappend mempty
-- Infix version of mappend
(<>) = mappendNote that mconcat is actually part of the class, although it has a default definition
defined in terms of mappend and mempty. As a result, instances of the
Monoid class need only to define those two primitives.
The next abstraction we covered in this guide was the Functor. Although we could give a
similar mathematical definition and translate it into Haskell, the mathematics is out of the scope
of this guide, so we can skip directly to the typeclass:
class Functor f where
fmap :: (a -> b) -> f a -> f b
-- Replace all locations in the input with the same value.
-- This may be overridden with a more efficient version.
(<$) :: a -> f b -> f a
(<$) = fmap . const
(<$>) :: (a -> b) -> f a -> f b
(<$>) = fmapThe Functor class Haskell uses defines an extra operation, <$. This operation
simply replaces the contents of the functor with a new value; thus, 3 <$ Just "hi" == Just 3.
For historical reasons, the similar operator <$> is exported from
Control.Applicative, even though it is quite idiomatic to use it with any Functor.
Once we’d seen a few functors, we looked at the workhorse of abstractions in Haskell – the
Monad typeclass. Like Functor and Monoid, the Monad typeclass
includes a few bits we haven’t previously discussed:
class Monad m where
-- Sequentially compose two actions, passing any value produced
-- by the first as an argument to the second.
(>>=) :: m a -> (a -> m b) -> m b
-- Sequentially compose two actions, discarding any value produced
-- by the first, like sequencing operators (such as the semicolon)
-- in imperative languages.
(>>) :: m a -> m b -> m b
-- | Inject a value into the monadic type.
return :: a -> m a
-- Fail with a message. This operation is not part of the
-- mathematical definition of a monad, but is invoked on pattern-match
-- failure in a 'do' expression.
fail :: String -> m a
-- Default definitions!
m >> k = m >>= \_ -> k
fail s = error sIn order to implement an instance of Monad, we need to define >>= and
return. The typeclass also contains >> (which is like >>= but discards
any value produced by its input) and fail, which is used on pattern match failures.
However, these are given default definitions defined in terms of >>= and error, so
they do not need to be implemented to make something into a Monad.