This is a continuation of Computing with Transistors, a series of blog posts describing how computers work from the ground up. I build upon my description of MOSFET transistors and logic gates from the previous post, Computing with Transistors.

In the previous post, we discussed how we could use transistors to build logic circuits, which could do simple boolean computations on their inputs. We can extend this practice without much difficulty to compute arbitrarily complicated boolean expressions. While this is great, on it's own, it's practically useless. What are we missing?

Memory

In order to perform computation and execute long-running programs, we need some form of storage. As it turns out, transistors are useful not only for logic, but also for storing data in a digital state! There are many ways to use transistors (sometimes with other elements, such as capacitors) to store memory, but the fundamental idea behind many of them is that the dynamic system that a network of transistors creates has a limited number of steady states in which it can reside. If this doesn't make sense now, it will in a moment. Let's go over a few different types of memory, and how we can build them out of circuit elements.

Flip-Flops

Before delving into flip-flops, let's quickly go over logic gates.

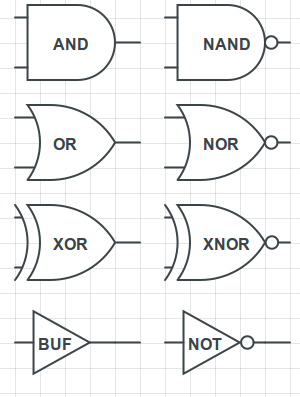
Logic gates. These are the most common and basic one and two-input gates.

These eight gates are the most common and most useful logic gates, and it's important to understand what each one does. In the previous blog post, we built NOR and NAND gates, which are depicted and labeled above. The rest of the gates are equally important, though:

• AND: An AND gate will output a "1" if and only if both of its inputs are "1". The inputs are given on the two wires coming in to the flat side of the gate (on the left), and the output is on the wire coming from the other side. It's important that you think of these logic gate diagrams as "flows of logic", or flows of truthiness, rather than circuits, because while they are instantiated as digital circuits, current does not flow along the wires that are drawn going in and out of the gates. The "1"s and "0"s are represented high low and high voltages, as we discussed in the previous post.
  
• OR: An OR gate will output a "1" if either of the inputs is a "1".
  
• XOR: A XOR (pronounced "ex-or" or "zor") gate will output a "1" if the two inputs are different from one another.
  
• NAND, NOR, XNOR: These gates are simply inverses of the previous three. Take the output of the previous three and negate it, and that's what these three will output. Note that XNOR is sometimes also called EQUIV, because it will output a "1" if and only if both of the inputs are the same (both are "0" or both are "1").
  
• NOT: A NOT gate takes its single input and outputs the opposite. If the input is a 1, it'll output a 0; if the input is a 0, it'll output a 1.
  
• BUF: A BUF gate is the logical complement of the NOT gate. It doesn't really do anything logical (it simply outputs the input that it is given), but you will occasionally find it in circuits because it can be used as a buffer. In other words, you can stick it along a circuit path in order to preserve the same voltage on both sides but to prevent current from flowing across the path.

Why are we going over gates, when we want to talk about memory? Well, a flip-flop is a type of memory which can be built directly out of logic gates. Here's what one type of flip-flop looks like:

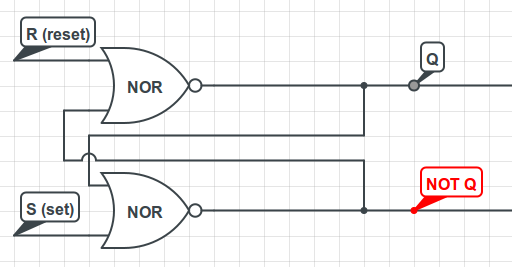
This is an SR flip flop. The S stands for "set" and the R stands for "reset". Turning them on "sets" and "resets" the state of the flip flop, respectively. We cannot turn both of them on.

What have we done? We've taken two NOR gates and fed the output of each one into the other one. This is a pair of cross-coupled NOR gates. Let's try to figure out what this does!

Suppose we let R = 0 and S = 1. What happens? Well, regardless of what Q is in the beginning, the output of the bottom gate must be "0". Thus, NOT Q = 0. Then, the output of the top gate is NOR(0, 0), which is 1. Thus, Q = 1. We have set the value inside the flip flop to be 1.

What if we let S drop down to 0? Well, nothing happens. If Q = 1 and R = S = 0, then the output of the bottom gate will be NOR(1, 0) = 0, while the output of the top gate will be NOR(0, 0) = 1. This is a stable configuration! The flip flop remembers Q. If you repeat the same analysis for Q = 0 and R = S = 0, you'll find that Q is remembered for Q = 0 as well.

Finally, if you let R = 1 and S = 0, you can trace the logic and you'll find that Q must become 0. That's why R is called the reset signal - it resets the value of Q to zero.

There's a pretty significant problem with this flip flop, though. We can't set both R = 1 and S = 1. It's pretty clear that that assignment makes no sense, though - what should the flip flop do if we try to set and reset it at the same time? For that reason, these flipflops - called SR flip flops - are rarely used in practice.

The most common type of flip flop used in practice is known as the D flip flop (with D standing for "data"). The D flip flop has an "enable" signal and a "data" signal. When the "enable" signal is on (high voltage, representing a "1"), the flip flop stores whatever data is coming in via the data signal. When the "enable" signal is turned off, the flip-flop simply remembers its state. There are many variations on this, such as the edge-triggered flip flop, which will only remember the state as the enable signal goes from low to high (and only at that edge!). Edge-triggered flip-flops are used all over the place in processor design, with the processor clock being the trigger that causes the flip-flop to read data in.

Flip-flops are very fast, in the sense that it takes very little time for signals to propagate all the way through a flip-flop. However, they're also incredibly expensive - it can take five to six gates to build a single flip-flop. With each gate taking 2-3 transistors, this can mean a total of 10-20 transistors for a single bit of memory. Not only is this expensive, but it also means we can't fit a lot of flip-flops in a small area, which is a requirement for having large memories. Due to these problems, flip-flops aren't used for large amounts of memory, but they are very common for things like internal processor registers and small register files.

SRAM

Flip-flops are great if you need to just store a few bytes of data, but what if you want megabytes? Gigabytes? Well, for that, you need some sort of RAM. One type of RAM is called SRAM, which stands for "static random access memory". As you'll see, this fares significantly better than flip-flops on cost - we can build a single bit of storage with only six transistors. Let's start by analyzing this "circuit":

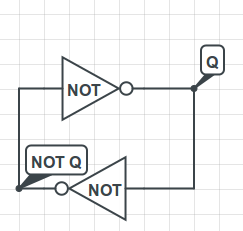
The basic idea behind SRAM is that two coupled inverters will reinforce each other and stay in whatever state they were originally put in.

This isn't a real circuit, but it serves to express the main point. Suppose Q = 0. Well, then NOT Q will obviously be 1. Which in turn means that Q will be 0. And so on, and so forth. If we somehow set Q and NOT Q, these coupled inverters will retain the same values of Q and NOT Q.

The real question is - how do we set the value of Q and NOT Q? Once we've done that, we have ourselves a piece of one-bit memory. We're going to do this by using two transistors to enable reading and writing from this memory cell, like this:

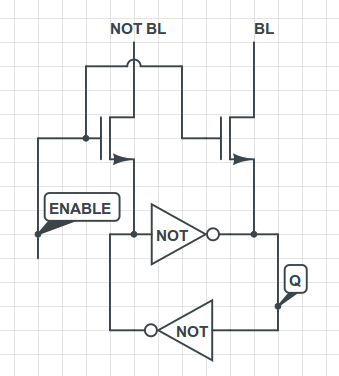
BL stands for "bit line". The enable signal is usually called WL, for "word line". The word line usually enables a whole word of memory (for example, 32 bits). The bit line, however, is specific to that bit.

In order to write to this piece of memory, we set the ENABLE signal to be high (to turn on both of those transistors) and then we set BL and NOT BL to the appropriate values, connecting those wires either to ground (low voltage) or Vdd (high voltage). These low and high voltages will override whatever state the coupled inverters are currently in, thus writing that values into the bit of memory.

In order to read from this piece of memory, we turn on the ENABLE signal, but we don't drive the bit lines (BL and NOT BL) with any voltage - instead, we let the inverters drive the bit lines. The inverters will set the value at the bit lines to either 0 or 1, depending on the state of the inverter pair, and we can use that value elsewhere in our circuit.

Wrap Up

There's quite a bit more to SRAM, though, that I won't go into. For instance, how are we arranging these bits of memory into a large swath of memory that we can access easily? We clearly can't wire every single bit of memory to some external output - that would take far too many wires. The circuitry that controls SRAM is also quite interesting, and I encourage you to read more about it (on Wikipedia, or elsewhere). You'll often find SRAM as embedded on-chip memory, or as processor caches. (I've been told that things like monitors or printers will usually use SRAM to store their temporary data, although I can't vouch for this, as I am an expert in neither monitors nor printers.)

In fact, there's quite a bit more to other types of memory as well. There are many more types of flip-flops, many of which are useful. There's another common type of memory called SDRAM, which uses a capacitor for its storage element, instead of coupled inverters. The great thing about SDRAM is that you can build it with fewer transistors, and therefore can have higher volumes of memory for lower costs. The price you pay is that you have to continually refresh the contents of the RAM every few microseconds, because otherwise the voltage in the capacitor slowly leaks away. SDRAM is usually more power-hungry than SRAM, precisely due to this constant refreshing that has to happen. (By the way, the DDR2/DDR3 RAM that you buy for your computer is SDRAM.)

Next Post

We've now talked about using transistors for computation and for memory. We've set the stage for some much more interesting topics. We can now use our fundamental units of hardware to build things such as multiplexers, decoders, or numeric adders and multipliers. In the next post, I'll discuss some of these basic hardware elements and number systems, which we're going to use to build our own computer processor. I'll introduce Verilog, a language we can use to describe hardware, so that we don't have to keep drawing incredibly complicated circuit diagrams. There's some really awesome stuff coming up!