Computing with Transistors

Any sufficiently advanced technology is indistinguishable from magic. - (Arthur C. Clarke)

For many years, I studied computers without ever understanding how they work. On the inside, a computer is a monstrously complex beast, with layers upon layers of abstraction which ultimately boil down to electrons running through silicon, obeying the fundamental laws of physics. We've built up so many layers of abstraction that the vast majority of people using computers - even the vast majority of highly technical programmers - don't know (and don't need to know!) how it all works on the inside. But while understanding every single layer of abstraction to its fullest extent is practically impossible, it's incredibly fascinating how modern computers are built and what physical principles allow them to function.

In this series of blog posts, I'd like to introduce you to many of the layers of abstraction bridging the gap between the laws of physics and assembly language. Given the rather large scope, I'm going to end up leaving out a lot of information about every topic I discuss. Just note that every topic I mention has, essentially, a field and a half solely devoted to it. With that said, let's begin with circuits.

Circuits

Fundamentally, all electronics operate on the basis of a set of equations known as Maxwell's equations, which dictate how electric and magnetic fields propagate. Particles known as electrons travel in the direction opposite the electric field, creating a current of electrons. Different types of materials have different effects upon electric fields and the movement of electrons, and this allows us to conjoin different materials to create circuits. The first important concept is that of a voltage source, or a battery. A voltage source is an abstraction which simply allows us to dictate the electric potential at a given point in the circuit, relative to some point in the circuit which we deem at zero potential (called ground). When thinking of electric potentials and currents, it can be very helpful to imagine an equivalent system but with a gravitational field instead of an electric field. In that analogous system, a voltage source is a hill with a bucket of water on it. The water has a lot of potential energy - if we allow it out of the bucket, it will gain energy and fall off the hill. Wires allow electrons to flow through them, towards higher potential and away from lower potential - just like pipes allow water to flow from higher regions to lower ones. As water flows from high to low, it can encounter resistance which slows down the current, such as a water wheel. In the same way, there is a circuit element called a resistor which prevents electrons from flowing through wires quickly. With these two elements (a voltage source and a resistor), we can draw a basic circuit:

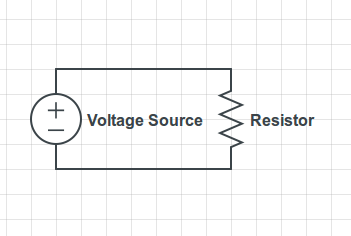
Current flows from high potential (the plus sign) to low potential (the minus sign). As it flows through the resistor, energy is dissipated as heat into the environment. Ohm's law says that the current is proportional to the voltage by a factor of \(1/R\), where \(R\) is the resistance.

This electrical circuit is analogous to a very similar "gravitational circuit":

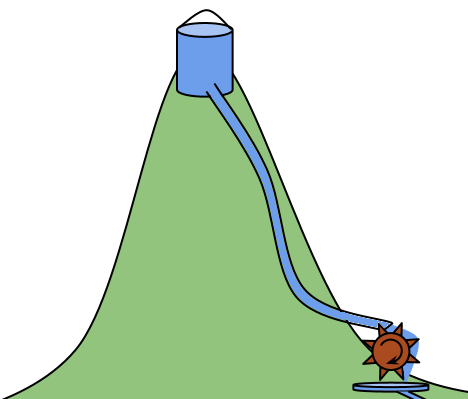
A "gravitational circuit" with a high potential (bucket of water on a hill) and current flowing from a high potential to a low potential through some resistance (in the form of a water wheel).

Mathematical analysis of circuits can be quite difficult, and there are many, many different circuit elements which can behave in very non-linear and confusing ways. However, the important thing is that you understand the concepts of voltage and current flow. When we analyze a circuit, we declare some point in that circuit to be our "ground" - in other words, its our reference point, just like "sea level" is a reference point for height. When we give the voltage at some point, we are always writing the potential energy with respect to ground (in the same way that maps give height above sea level). Current is the movement of electrons and goes from high voltage to low voltage, like rivers flowing from mountains to the sea. Wires are just connections between different places, and act like horizontal pipes for water, offering no resistance to current and no change in voltage.

So, then, how can we use circuits to build a computer? We've still got a ways to go.

The Transistor

Resistors simply dissipate energy as electrons flow through them. There are other circuit elements called capacitors which can store charge as it flows through them, and later discharge it. There are many other circuit elements, but the one that all digital electronics are based off of is called the MOSFET transistor. (There are other types of transistors, but they are rarely used in digital electronics.)

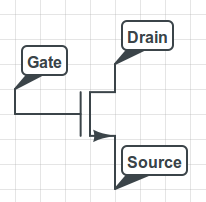
(N-ch) MOSFET transistor with 3 ports: a gate, where the control signal is applied; a drain, connected to a high potential; and a source, connected to a lower potential. Counterintuitively, current actually flows from the drain to the source, not the other way around. (However, electrons flow from the source to the drain. Remember that current flows opposite the direction of electron flow, since electrons are negative current!)

When operated as a digital element, the transistor can be modeled as a switch, which acts like a wire or an open circuit (no connection), depending on whether the switch is turned on. It has a control signal, which is applied as a voltage at the gate, which turns the switch on or off. We then connect one end of the transistor to a voltage supply (which can be thought of as an energy source) and the other to ground (a place for the energy to go). When the voltage at the gate is high, it allows current to flow through the transistor unhindered. When the gate voltage is low, it acts like a broken wire and current cannot flow through it.

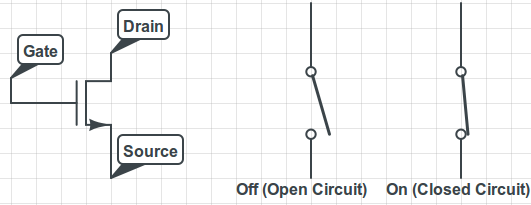
Left: MOSFET circuit element; Center: transistor with low gate voltage acts like an open circuit; Right: transistor with high voltage acts like a wire with very low resistance.

The wonderful thing about transistors is that we can use them to perform digital calculations on our input signal. Let's measure the voltage (as a function of input voltage) on the side of the transistor that is farther away from ground, like this:

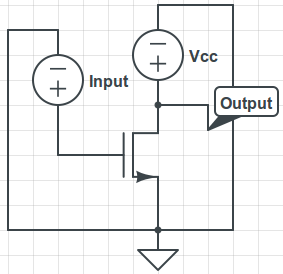
Transistor with power at the drain with voltage Vcc and some input voltage applied at the gate. We represent the ground point of the circuit with the symbol at the source port of the transistor. Sometimes, circuit diagrams will have multiple ground symbols - these are just shorthand to avoid drawing grounding wires all over the diagram. The output is given by the voltage measured at the point labeled "Output".

What happens if our input voltage is high? If the input voltage is high, then the transistor happily allows current to pass, and just acts like a wire. Since the transistor offers no (well, in really, very little) resistance, the voltage we measure is low. What happens if our input voltage is low? In this case, the transistor refuses to let current pass, so all the energy remains pent up away from ground, and the voltage we measure is high. We just built a logic inverter! It takes the logical value from our input signal and inverts it (high becomes low, low becomes high). If we encode "0" bits as low voltage and "1" bits as high voltage, we just built a one-bit binary NOT gate.

What else can we do? Turns out we can build AND gates and OR gates too. For example, what does this circuit do?

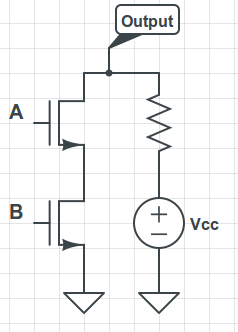
We use voltages A and B as inputs, and measure the output as usual. Note that there is a resistor here - while it wasn't included on the previous diagram, it is absolutely necessary, otherwise we get a short-circuited ideal voltage source, which is nonsensical. In this diagram and with our simplified model, when A and B are both high, the entire voltage drop is over the resistor, which prevents the current from being infinite.

The only way this will output a low voltage (a zero) is if both transistors act like wires, which happens if both the input signals are one (high). This is a NAND gate! Using a parallel connection instead of a serial connection, we can build a NOR gate:

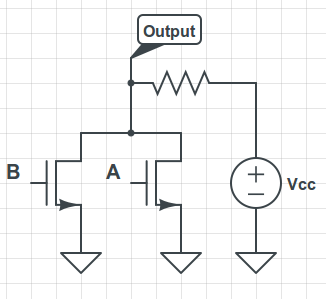
This time, we have two parallel transistors, and if either A or B are high, then there is a path from Vcc to ground. If both are low, then there is no path and thus no current, so the output voltage is high.

The only way this outputs a one (high voltage) is if both of the input voltages are zero. If either input is high, the transistor becomes a short circuit, and current can pass from the battery to ground. As an exercise, draw the diagrams for AND and OR gates. (You can chain gates by connecting the output of one gate to the input of another!)

(Note that this isn't actually the full story - in reality, there are two types of MOSFETS which use differently doped semiconductors, called p-channel and n-channel MOSFET transistors. Then, CMOS (complementary MOS) gates are built by using both types of transistors, because some types are good for passing high voltages and others are good for passing low voltages. Most microprocessors use CMOS gates.)

In this way, transistors allow us to build logic gates. In addition to logic gates, we can use transistors to build memory (RAM), registers, and many of the other electrical components necessary to build modern digital systems.

We've now scaled two abstraction levels. The first one got us from the laws of physics (Maxwell's equations, electric fields, and so on) to circuit diagrams (voltage sources, resistors, and transistors). The second abstraction level used transistors to get us from circuit diagrams to logic gates such as NOT gates, AND gates, and OR gates. In the next post, we'll discuss some methods for jumping the abstraction ladder from logic gates to stateful digital circuits and numbers.